Cauchy-Riemannsche Differentialgleichungen
Schlagen Sie auch in anderen Wörterbüchern nach:
Cauchy-Riemannsche partielle Differentialgleichungen — Die Cauchy Riemannschen partiellen Differentialgleichungen (nach Augustin Louis Cauchy und Bernhard Riemann) sind ein Begriff aus der Funktionentheorie und ein Kriterium für komplexe Differenzierbarkeit. Die Gleichungen wurden das erste Mal 1814… … Deutsch Wikipedia
Komplexe Analysis — Die Funktionentheorie ist ein Teilgebiet der Mathematik. Sie befasst sich mit den differenzierbaren komplexwertigen Funktionen komplexer Variablen. Gebräuchlich ist auch die Bezeichnung komplexe Analysis. Inhaltsverzeichnis 1 Komplexe Funktionen… … Deutsch Wikipedia
Bernhard Riemann — 1863 Georg Friedrich Bernhard Riemann (* 17. September 1826 in Breselenz bei Dannenberg (Elbe); † 20. Juli 1866 in Selasca bei Verbania am Lago Maggiore) war ein deutscher Mathematiker, der … Deutsch Wikipedia
Kramers-Kronig-Relation — Die Kramers Kronig Beziehungen (nach Hendrik Anthony Kramers und Ralph Kronig) setzen Real und Imaginärteil bestimmter meromorpher Funktionen in Form einer Integralgleichung miteinander in Beziehung. Sie stellen einen Spezialfall der Hilbert… … Deutsch Wikipedia
Kramers-Kronig-Relationen — Die Kramers Kronig Beziehungen (nach Hendrik Anthony Kramers und Ralph Kronig) setzen Real und Imaginärteil bestimmter meromorpher Funktionen in Form einer Integralgleichung miteinander in Beziehung. Sie stellen einen Spezialfall der Hilbert… … Deutsch Wikipedia
Kramers-Kronig-Transformation — Die Kramers Kronig Beziehungen (nach Hendrik Anthony Kramers und Ralph Kronig) setzen Real und Imaginärteil bestimmter meromorpher Funktionen in Form einer Integralgleichung miteinander in Beziehung. Sie stellen einen Spezialfall der Hilbert… … Deutsch Wikipedia
Kramers-Krönig-Relation — Die Kramers Kronig Beziehungen (nach Hendrik Anthony Kramers und Ralph Kronig) setzen Real und Imaginärteil bestimmter meromorpher Funktionen in Form einer Integralgleichung miteinander in Beziehung. Sie stellen einen Spezialfall der Hilbert… … Deutsch Wikipedia
Georg Friedrich Bernhard Riemann — Bernhard Riemann Georg Friedrich Bernhard Riemann (* 17. September 1826 in Breselenz bei Dannenberg (Elbe); † 20. Juli 1866 in Selasca bei Verbania am Lago Maggiore) war ein deutscher Mathem … Deutsch Wikipedia
Liste von Mathematikern — Diese Liste bedeutender Mathematiker stellt eine Auswahl von Mathematikern von der Antike bis zu Gegenwart dar. Die Auswahl der Mathematiker richtet sich dabei nach ihren wissenschaftlichen Leistungen oder ihrem Bekanntheitsgrad, aufgrund deren… … Deutsch Wikipedia
Liste bedeutender Mathematiker — Diese Liste bedeutender Mathematiker stellt eine Auswahl von Mathematikern von der Antike bis zu Gegenwart dar. Die Auswahl der Mathematiker richtet sich dabei nach ihren wissenschaftlichen Leistungen oder ihrem Bekanntheitsgrad, aufgrund deren… … Deutsch Wikipedia
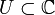 offen und
offen und 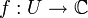 eine komplexwertige Funktion einer komplexen Variablen. In kanonischer Weise kann man eine komplexe Zahl
eine komplexwertige Funktion einer komplexen Variablen. In kanonischer Weise kann man eine komplexe Zahl 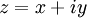 mit
mit 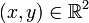 identifizieren. Sei
identifizieren. Sei 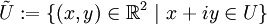 das entsprechende Pendant zu U im
das entsprechende Pendant zu U im 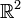 und
und 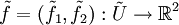 definiert vermöge
definiert vermöge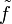 im folgenden Sinne:
im folgenden Sinne: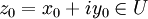 . Dann sind äquivalent:
. Dann sind äquivalent: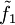 und
und 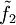 nach x und y die in (x0,y0) stetig sind, und es gelten die Cauchy-Riemann'schen Differentialgleichungen
nach x und y die in (x0,y0) stetig sind, und es gelten die Cauchy-Riemann'schen Differentialgleichungen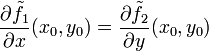 und
und 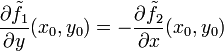 .
.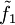 und
und 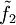 harmonische Funktionen sind, sofern f holomorph ist.
harmonische Funktionen sind, sofern f holomorph ist.