Cauchy-Riemann-Differentialgleichungen
Schlagen Sie auch in anderen Wörterbüchern nach:
Cauchy-Riemannsche Differentialgleichungen — Die Cauchy Riemann schen partiellen Differentialgleichungen (nach Augustin Louis Cauchy und Bernhard Riemann) sind ein Begriff aus der Funktionentheorie und ein Kriterium für komplexe Differenzierbarkeit. Die Gleichungen wurden das erste Mal 1814 … Deutsch Wikipedia
Cauchy-Riemann-Gleichungen — Die Cauchy Riemann schen partiellen Differentialgleichungen (nach Augustin Louis Cauchy und Bernhard Riemann) sind ein Begriff aus der Funktionentheorie und ein Kriterium für komplexe Differenzierbarkeit. Die Gleichungen wurden das erste Mal 1814 … Deutsch Wikipedia
Cauchy-Riemannsche partielle Differentialgleichungen — Die Cauchy Riemannschen partiellen Differentialgleichungen (nach Augustin Louis Cauchy und Bernhard Riemann) sind ein Begriff aus der Funktionentheorie und ein Kriterium für komplexe Differenzierbarkeit. Die Gleichungen wurden das erste Mal 1814… … Deutsch Wikipedia
Augustin Louis Cauchy — [ogysˈtɛ̃ lwi koˈʃi] (* 21. August 1789 in Paris; † 23. Mai 1857 in Sceaux) war ein französischer Ma … Deutsch Wikipedia
Cauchy-Problem — Als Anfangswertproblem (AWP) (manchmal auch als Anfangswertaufgabe (AWA) oder Cauchy Problem genannt) bezeichnet man in der Analysis eine wichtige Klasse von Differentialgleichungen, bei denen aus vorgegebenen Anfangsdaten, nämlich dem… … Deutsch Wikipedia
Bernhard Riemann — 1863 Georg Friedrich Bernhard Riemann (* 17. September 1826 in Breselenz bei Dannenberg (Elbe); † 20. Juli 1866 in Selasca bei Verbania am Lago Maggiore) war ein deutscher Mathematiker, der … Deutsch Wikipedia
Georg Friedrich Bernhard Riemann — Bernhard Riemann Georg Friedrich Bernhard Riemann (* 17. September 1826 in Breselenz bei Dannenberg (Elbe); † 20. Juli 1866 in Selasca bei Verbania am Lago Maggiore) war ein deutscher Mathem … Deutsch Wikipedia
Pseudoholomorphe Kurve — Pseudoholomorphe Kurven (PHK) bezeichnen in der symplektischen Topologie eine glatte Abbildung von einer Riemannfläche in eine fast komplexe Mannigfaltigkeit, die die Cauchy Riemann Differentialgleichungen erfüllt. Sie wurden 1985 durch Mikhail… … Deutsch Wikipedia
Absolutbetrag — Verlauf der Absolutbetragsfunktion auf In der Mathematik ordnet die Betragsfunktion einer reellen oder komplexen Zahl ihren Abstand zur Null zu. Dieser sogenannte absolute Betrag, Absolutwert oder auch schlicht Betrag ist immer eine nichtnegative … Deutsch Wikipedia
Absolute Zahl — Verlauf der Absolutbetragsfunktion auf In der Mathematik ordnet die Betragsfunktion einer reellen oder komplexen Zahl ihren Abstand zur Null zu. Dieser sogenannte absolute Betrag, Absolutwert oder auch schlicht Betrag ist immer eine nichtnegative … Deutsch Wikipedia
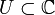 offen und
offen und 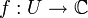 eine komplexwertige Funktion einer komplexen Variablen. In kanonischer Weise kann man eine komplexe Zahl
eine komplexwertige Funktion einer komplexen Variablen. In kanonischer Weise kann man eine komplexe Zahl 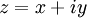 mit
mit 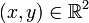 identifizieren. Sei
identifizieren. Sei 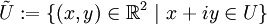 das entsprechende Pendant zu U im
das entsprechende Pendant zu U im 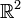 und
und 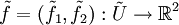 definiert vermöge
definiert vermöge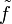 im folgenden Sinne:
im folgenden Sinne: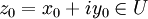 . Dann sind äquivalent:
. Dann sind äquivalent: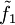 und
und 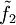 nach x und y die in (x0,y0) stetig sind, und es gelten die Cauchy-Riemann'schen Differentialgleichungen
nach x und y die in (x0,y0) stetig sind, und es gelten die Cauchy-Riemann'schen Differentialgleichungen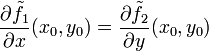 und
und 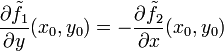 .
.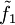 und
und 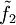 harmonische Funktionen sind, sofern f holomorph ist.
harmonische Funktionen sind, sofern f holomorph ist.