Japanischer Satz für Sehnenvierecke

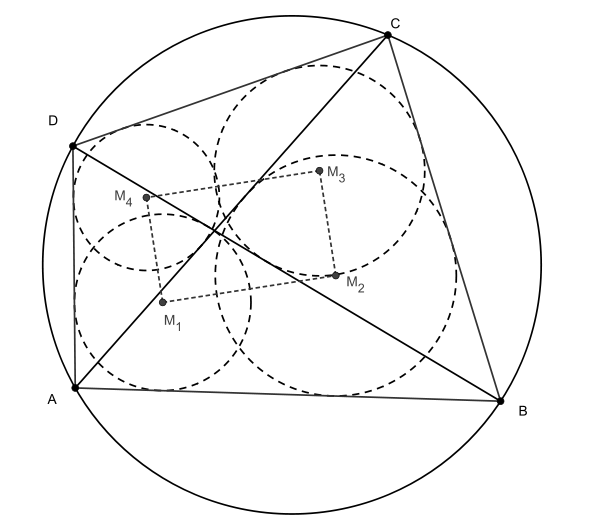
Der japanische Satz (engl. Japanese Theorem) besagt, dass in einem Sehnenviereck die Mittelpunkte der vier Inkreise der vier Dreiecke, die sich durch Triangulierung mit den Diagonalen ergeben, die Eckpunkte eines Rechtecks bilden.

Sei $\square ABCD$ ein beliebiges Sehnenviereck und seien M₁,M₂,M₃,M₄ die Mittelpunkte der Inkreise der Dreiecke $\triangle ABD, \triangle ABC, \triangle CDB, \triangle CDA$. Dann bilden M₁,M₂,M₃,M₄ ein Rechteck.

Siehe auch

• Satz von Carnot
• Sangaku
• Wasan
• Japanischer Satz für konzyklische Polygone

Weblinks

• japanischer Satz - Geschichte des Theorems (engl.)
• japanischer Satz bei Cut-the-Knot
•  Wikibooks: Beweisarchiv - Japanischer Satz für konzyklische Vierecke – Lern- und Lehrmaterialien