Kugelschicht

Kugelschicht

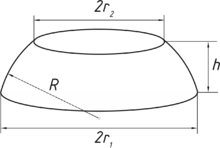
Eine Kugelschicht, auch Kugelscheibe genannt, ist ein Teil der Vollkugel. Sie hat zwei parallele Schnittflächen. Anschaulich kann man sich das so vorstellen, dass man von einem (als kugelförmig angenommenen) Apfel aus der Mitte eine Scheibe herausschneidet.

Mathematische Präzisierung

Die Kugelschicht wird aus einer Vollkugel (deren Radius sei R) durch zwei parallele, die Kugel echt schneidende Ebenen (ihr Abstand sei h) herausgeschnitten.

Zur Berechnung werden ein paar Bezeichnungen benötigt:

Die größere der beiden durch den Schnitt entstehenden parallelen Kreisflächen wird Grundfläche genannt und mit dem Buchstaben G bezeichnet, ihr Radius sei r₁. Die kleinere ^[1] wird Deckfläche genannt und mit dem Buchstaben D bezeichnet, ihr Radius sei r₂. Die dritte der begrenzenden Flächen, die Mantelfläche, wird auch Kugelzone genannt und durch M bezeichnet.

Formeln

Eigenschaft	Formel
Flächeninhalt der Kugelzone M[2]	M = 2πRh
Flächeninhalt der Grundfläche G der Kugelschicht	$G=\pi r_1^2$
Flächeninhalt der Deckfläche D der Kugelschicht	$D=\pi r_2^2$
Flächeninhalt der Oberfläche S der Kugelschicht	$S=\pi(2Rh+ r_1^2+r_2^2 )$
Volumen V der Kugelschicht	$V=\frac {\pi h}{6}( 3r_1^2+3r_2^2+h^2)$
Zusammenhang zwischen R,r1, r2 und h	$R^2=r_1^2+ \left (\frac{r_1^2-r_2^2-h^2}{2h}\right ) ^2$

Kugelschicht mit Mantellinie des einbeschriebenen Kegelstumpfes

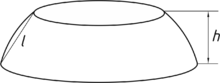
Ist V₁ das Volumen des Kegelstumpfes, der einer Kugelschicht einbeschrieben ist und l die Länge seiner Mantellinie, so ist

$V-V_1 = \frac{1}{6} \pi hl^2$

Herleitung der Formeln

Flächeninhalt der Kugelzone

Schnitt durch eine Kugelschicht

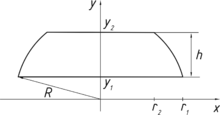
Die Kugelzone wird erzeugt, indem der Rand der Querschnittsfläche um die y-Achse rotiert. Für den Flächeninhalt gilt dann ^[3] $\begin{align} M & =2 \pi \int\limits_{y_1}^{y_2} x \cdot \sqrt {1+ \left (\frac {\,dx}{\,dy} \right )^2} \,dy \\ & =2 \pi \int\limits_{y_1}^{y_2} \sqrt {R^2-y^2} \cdot \sqrt {1+ \left (\frac {-y}{\sqrt{R^2-y^2}} \right )^2} \,dy \\ & =2 \pi \int\limits_{y_1}^{y_2} \sqrt{R^2-y^2} \cdot \sqrt {1+ \frac {y^2}{R^2-y^2}} \,dy \\ & =2 \pi \int\limits_{y_1}^{y_2} \sqrt{R^2-y^2+y^2} \,dy \\ & = 2 \pi R \int\limits_{y_1}^{y_2} \,dy \\ & = 2 \pi R (y_2 -y_1) \\ & = 2 \pi R h \end{align}$

Volumen der Kugelschicht

Die Kugelschicht wird erzeugt, indem deren Querschnittsfläche um die y-Achse rotiert. Für das Volumen gilt dann ^[3]

$\begin{align} V & = \pi \int\limits_{y_1}^{y_2} x^2 \,dy \\ & = \pi \int\limits_{y_1}^{y_2} (R^2-y^2)^2 \,dy \\ & = \pi \left( R^2y-\frac {1}{3}y^3 \right) \\ & = \pi \left(R^2y_2 - \frac{1}{3} y_2^3 - R^2y_1 + \frac{1}{3} y_1^3 \right) \\ & = \pi \left[R^2 \underbrace{(y_2 - y_1)}_{h} - \frac{1}{3} (y_2^3-y_1^3) \right] \\ & = \pi \left[R^2h- \frac{1}{3} \underbrace{(y_2 - y_1)}_{h}(y_2^2+y_2y_1+y_1^2) \right] \\ & = \frac{\pi h}{6} \left[6R^2-2y_2^2-2y_2y_1-2y_2^2 \right] \\ & = \frac{\pi h}{6} \left[3R^2-3y_2^2 + 3R^2 -3y_1^2 + y_2^2 -2y_2y_1+y_1^2 \right] \text { (Hier wird mit} -y_2^2-y_1^2+y_2^2+y_1^2 \text {erweitert)} \\ & = \frac{\pi h}{6} \left[3 \underbrace {(R^2-y_2^2)}_{r_2^2} + 3 \underbrace {(R^2 -y_1^2)}_{r_1^2} + (\underbrace {y_2-y_1}_{h})^2 \right] \\ & = \frac{\pi h}{6} (3r_1^2+3r_2^2+h^2) \\ \end{align}$

Siehe auch

• Kugelkalotte
• Kugelring
• Kugelausschnitt

Literatur

• I. Bronstein u.a.: Taschenbuch der Mathematik. Harri Deutsch, Frankfurt 2001, ISBN 3-8171-2005-2.
• L. Kusch u.a.: Mathematik, Teil 4 Integralrechnung. Cornelsen, Berlin 2000, ISBN 3-464-41304-7.

Weblinks

• Eric W. Weisstein: Spherical Segment. In: MathWorld. (englisch)
• Eric W. Weisstein: Spherical zone. In: MathWorld. (englisch)

Einzelnachweise

1. ↑ Die Formeln gelten auch, wenn die Kugel symmetrisch geschnitten wird und es zwei gleich große Schnittflächen gibt.
2. ↑ Lit.: Formeln nach Bronstein, 2000
3. ↑ ^{a b} Lit.: Herleitung nach Kusch, 2000