- Kugelring
-
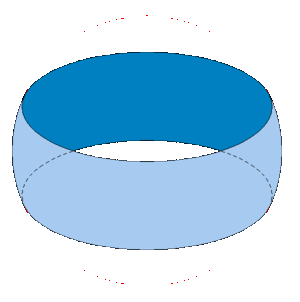
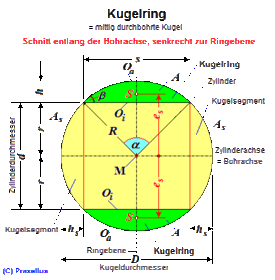
Der Kugelring ist eine zylindrisch durchbohrte Kugel. Der deutsche Begriff Kugelring wird in der Mathematik in Analogie zum Kreisring verwendet. Im englischen Sprachraum ist der Begriff Spherical Ring [1] dafür üblich. Bild 1 zeigt den Kugelring in einer schrägen Draufsicht. Die rote Linie stellt den Umriss der zugehörigen Kugel dar. Mathematisch gesehen handelt es sich beim Kugelring um eine Durchdringung von Kugel und Zylinder, wobei die Zylinderachse durch den Kugelmittelpunkt geht und das vom Zylinder verdrängte Kugelvolumen (in Bild 2 gelb gekennzeichnet) subtrahiert wird. Von der Kugel bleibt dann nur ein Ring übrig, dessen Querschnitt (in Bild 2 grün gekennzeichnet) aus einem Kreissegment (Kreisabschnitt) besteht.
Inhaltsverzeichnis
Geometrie und Formeln
Bild 2 zeigt einen Schnitt durch den Kugelring in der Zylinderachse (Bohrachse). Die grünen Kreissegmente sind die Querschnittsflächen des Ringes und die gelbe Fläche stellt den Längsschnitt des herausgebohrten Körpers dar, der aus einem Zylinder mit der Länge s und zwei Kugelsegmenten mit der Höhe hs und dem Zylinderradius r besteht.
Geometrische Elemente
Die Zeichnung (Bild 2) gibt die Lage der Elemente mit den Bezeichnungen an, die zur Erläuterung der nachstehenden Formeln gebraucht werden. Die Tabelle gibt die Formelzeichen und deren Bedeutung an.

Kugelmittelpunkt 
Flächenschwerpunkt des Ringquerschnitts 
Kugelradius = Außenradius des Kugelrings 
Kugeldurchmesser 
Bohrlochradius = Innenradius des Kugelrings 
Bohrlochdurchmesser = Zylinderdurchmesser 
Ringbreite = Sehne des Kreissegments 
Höhe des Kreissegments = Dicke des Rings 
Zentriwinkel des Bogens über der Sehne s in Altgrad (°) 
Berechnung des Winkels 
Flankenwinkel des Kugelrings bezogen auf die Sehne s in Altgrad (°) 
Schwerpunktabstand [2] des Kreissegments vom Kreismittelpunkt 
Fläche des Kreissegments (= Ringquerschnitt) Volumen des Kugelrings
Das Volumen des Kugelrings ist der Rauminhalt, der außen von einem Teil der Kugeloberfläche (Kugelzone der Höhe s, symmetrisch zum Mittelpunkt der Kugel) und innen vom Mantel des herausgeschnittenen Zylinders der Länge s begrenzt wird.
Die nachfolgende Formel für die Berechnung des Volumens leitet man als Rotationskörper her, indem man das in der Zeichnung grün gekennzeichnete Kreissegment (den Querschnitt des Kugelrings) mit seinem Schwerpunktabstand es um die Zylinderachse kreisen lässt.
Es sei s die Sehne des Kreissegments und zugleich die Ringbreite des Kugelrings. Die Fläche A des Kreissegments muss nicht berechnet werden, weil sie sich bei der Herleitung herauskürzt.
Das Volumen Vr des Rotationskörpers Kugelring berechnet man nach der Formel:
 ,
,
also:
 .
.
Lehrsatz
Aus der Formel für das Volumen des Kugelrings folgert man den Lehrsatz:
- Alle Kugelringe mit gleicher Breite s haben das gleiche Volumen.
- Das Volumen Vr eines beliebig großen Kugelrings wird allein durch die Ringbreite s bestimmt.
Es ist ein überraschendes Phänomen, dass sich unter Beibehalten der Ringbreite s und bei beliebiger Vergrößerung oder Verkleinerung des Halbmessers R der Kugel das Volumen des Kugelrings nicht ändert, nur die Ringdicke h ändert sich entsprechend. Gleiches Volumen bedeutet bei gleichem Material auch gleiches Gewicht und gleiche Masse. Kugelringe mit gleicher Breite und aus gleichem Material sind also alle gleich schwer.
Verhältnis der Volumina von Kugelring und Kugel
Das Verhältnis des Kugelringvolumens Vr zum Kugelvolumen Vk wird nur durch die Ringbreite s und den Kugeldurchmesser D bestimmt:
 .
.
Sonderfall: Eine Kugel mit dem Durchmesser s hat das gleiche Volumen wie ein Kugelring mit der Breite s. Die Kugel ist ein unechter Kugelring, denn man kann die Kugel als Kugelring mit der Bohrung r = 0 betrachten und berechnen.
Oberfläche des Kugelrings
Es seien R der Kugelradius und r der Radius des (ausgebohrten) Zylinders, dann ergibt sich die Ringaußenfläche Oa als Kugelzone nach der Formel:
und die Ringinnenfläche Oi als Mantel des Zylinders nach der Formel:
Die Gesamtoberfläche Or des Kugelrings beträgt:
Flankenwinkel der Ringkante
Je größer der Kugelring, desto kleiner ist der Flankenwinkel
 der Ringkante, der auf die Sehne s bezogen wird:
der Ringkante, der auf die Sehne s bezogen wird:Praktische Anwendung
Der Kugelring wird in der Technik dazu verwendet, um für ein Kugelgelenk, das mit einer im Kugelring verschieblichen zylindrischen Stange verbunden ist, vier Freiheitsgrade des Stangenendpunktes zu erreichen: Bewegungen in der x-, y- und z-Richtung, sowie eine Drehung der zylindrischen Stange um die eigene Längsachse.
Einzelnachweise
- ↑ Spherical Ring
- ↑ Bartsch, Hans-Jochen: Mathematische Formeln, 10. Auflage, 1971, Buch- und Zeitverlagsgesellschaft mbH, Köln, ohne ISBN, S. 149
Literatur
- Gardner, M.: Hexaflexagons and Other Mathematical Diversions: The First Scientific American Book of Puzzles and Games (1959, 1988; University of Chicago Press, ISBN 0226282546, Seiten 113-121)
- Weisstein, Eric W.: Spherical Ring. From MathWorld--A Wolfram Web Resource; siehe Spherical Ring.
- Bartsch, Hans-Jochen: Mathematische Formeln, 10. Auflage, 1971, Buch- und Zeitverlagsgesellschaft mbH, Köln,ohne ISBN.
Siehe auch
Weblinks
Wikimedia Foundation.