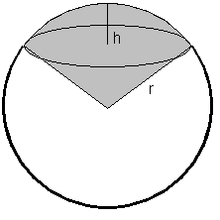
Kugelausschnitt

Kugelausschnitt

Ein Kugelausschnitt oder Kugelsegment bezeichnet in der Mathematik einen kegelartigen Ausschnitt vom Zentrum einer Kugel bis zu ihrer Oberfläche.

Herleitung des Volumens

Zur Berechnung des Volumens nimmt man eine Unterteilung in 2 Körper vor: Kegel und Kugelabschnitt.

I) Volumen des Kegels

Der Kegel kann als ein Rotationskörper mit der Randfunktion $y = \frac {R}{r-h}x = \frac {\sqrt{2rh-h^2}}{r-h}x$ betrachtet werden.

Den Term für R erhält man über den Kathetensatz. Das Volumen eines Rotationskörpers ist $V = \pi \int_{a}^{b} y^2 \mathrm dx$

Setzt man nun die Gleichung für die Randfunktion und die Integrationsgrenzen ein und löst auf, erhält man das Volumen des Rotationskörpers.

$V_1 = \pi \int_{0}^{r-h} \left( \frac{\sqrt{2rh-h^2}}{r-h}x\right) ^2 \mathrm dx$

$V_1 = \pi \int_{0}^{r-h} \frac{2rh-h^2}{(r-h)^2}x^2 \mathrm dx$

$V_1 = \pi \frac{2rh-h^2}{(r-h)^2} \left[ \frac{1}{3}x^3 \right]_{0}^{r-h}$

$V_1 = \pi \frac{2rh-h^2}{(r-h)^2} \frac{1}{3}(r-h)^3$

$V_1 = \frac{\pi}{3}(2rh-h^2)(r-h)$

Man kann sich von der Richtigkeit der Formel leicht überzeugen, indem man mit der Formel für das Volumen des Kegels vergleicht, wobei 2rh − h² dem dortigen Radius ins Quadrat r² entspricht und r − h der Höhe h.

II) Volumen des Kugelabschnittes

Auch der Kugelabschnitt wird als Rotationskörper betrachtet. Die Randfunktion erhält man entweder, indem man Kreisgleichung y² = r² − x² auf unseren Fall anwendet:

$\begin{align} y^2 = r^2-(r-x)^2 = r^2 -(r^2-2rx+x^2) = 2rx-x^2 \end{align}$

$\begin{align}y = \sqrt{ 2rx-x^2 }\end{align}$

oder die oben bereits benutzte Herleitung über den Kathetensatz benutzt: $R=\sqrt{2rh-h^2}$, wobei das h mit der Veränderlichen x ersetzt wird.

Nun wird wieder in die Gleichung des Rotationsvolumens eingesetzt und aufgelöst:

$V = \pi \int_{a}^{b} y^2 \mathrm dx$

$V_2 = \pi \int_{0}^{h} 2rx-x^2 \mathrm dx$

$V_2 = \pi \left[ rx^2-\frac{1}{3}x^3\right]_{0}^{h}$

$V_2 = \pi \left( rh^2-\frac{1}{3}h^3\right)$

$V_2 = \frac{\pi}{3} \left( 3rh^2-h^3\right)$

III) Zusammenfassung beider Volumina

$V= V_1 + V_2 =\frac{\pi}{3}(2rh-h^2)(r-h) + \frac{\pi}{3} \left( 3rh^2-h^3\right)$

$V= \frac{\pi}{3}(2r^2h-2rh^2-h^2r+h^3) + \frac{\pi}{3} \left( 3rh^2-h^3\right)$

$V= \frac{\pi}{3}(2r^2h-2rh^2-rh^2+h^3+3rh^2-h^3)$

$V= \frac{\pi}{3}(2r^2h)$

$V= \frac{2 \pi r^2 h}{3}$

Siehe auch

• Kugelkalotte
• Kugelring
• Kugelschicht

Weblinks

• Eric W. Weisstein: Spherical sector. In: MathWorld. (englisch)
• Eric W. Weisstein: Spherical cone. In: MathWorld. (englisch)