Dichteste Kugelpackung

Eine dichteste Kugelpackung ist die geometrische Anordnung unendlich vieler Kugeln gleicher Größe, so dass die größtmögliche Dichte erzielt wird, also der Anteil an Leerraum minimal ist. Eine solche Anordnung ergibt sich, wenn viele Kugeln schichtweise gestapelt werden. Innerhalb einer Schicht berührt dabei jede Kugel sechs Nachbarkugeln. Die Packungsdichte einer dichtesten Kugelpackung ist:

$\frac{\pi}{3\sqrt 2} \approx 0{,}74048 \approx 74%$

Johannes Kepler vermutete 1611, dass dies die größtmögliche Packungsdichte einer beliebigen Anordnung von unendlich vielen Kugeln im 3-dimensionalen Raum ist. Diese Keplersche Vermutung wurde 1831 von Carl Friedrich Gauß für Anordnungen bewiesen, bei denen die Kugeln auf einem Gitter liegen. Für den Fall beliebiger Anordnungen gibt es seit 1998 einen Computerbeweis, der von der Fachwelt jedoch noch nicht vollständig anerkannt ist.

Die Betrachtung einer endlichen Zahl von Kugeln führt zur Theorie der endlichen Kugelpackungen, einem nicht weniger komplexen Problem der Mathematik.

Dichteste Kugelpackungen treten in Kristallstrukturen auf und sind daher in der Kristallographie und in der Werkstoffkunde und Kristallchemie von Bedeutung.

Struktur

Schwarz: die A-Schicht
Rot: die B-Schicht
Blau: die C-Schicht

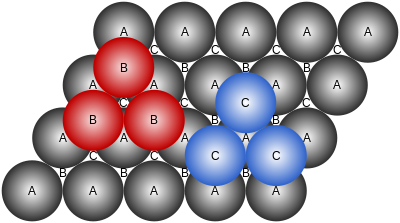
Eine dichteste Kugelpackung besteht aus hexagonalen Kugel-Schichten. In einer dieser Schichten (mit A gekennzeichnet) gibt es zwei Arten dreieckiger Leerstellen, eine mit der Spitze nach unten (mit B gekennzeichnet) und eine mit der Spitze nach oben (mit C gekennzeichnet). Auf diese Schicht kann jetzt eine weitere hexagonal dichtest gepackte Kugelschicht so gelegt werden, dass alle Kugeln entweder in den B- oder den C-Lücken sitzen. Eine Struktur, die durch eine entsprechende Stapelung dieser Kugelschichten entsteht, wobei dieselbe Schicht nicht zweimal aufeinander folgen darf, heißt dichteste Kugelpackung. Üblicherweise wird sie durch die Reihenfolge der Stapel beschrieben. Es gibt prinzipiell unendlich viele Möglichkeiten für die Bildung einer dichtesten Kugelpackung. Unabhängig von der Reihenfolge der Schichten berührt dabei jede Kugel immer 12 Nachbarn (Kusszahl: 12), sechs in der eigenen Schicht, sowie drei je in der darüberliegenden und der darunterliegenden.

Stapelt man die Schichten in einer beliebigen Reihenfolge aufeinander, so hat der Kristall mindestens eine dreizählige Achse in Stapelrichtung. Er hat damit mindestens die Punktgruppe $\ P3m1$ oder $\ R3m1$. Bei entsprechender Stapelung können aber auch höhersymmetrische Strukturen entstehen. Insgesamt sind folgende 9 Punktgruppen möglich: $\ P3m1, \, P\bar3 m1, \, P\bar6 m2, \, P6_3 mc, \, P6_3/mmc, \, R3m1, \, R\bar 3m1, \,F\bar4 3m, \, Fm\bar 3 m$.

Bedeutung

Die Anordnung von Atomen in einer dichtesten Kugelpackung entspricht einem wichtigen Grundprinzip bei der Bildung von Kristallen: dem Prinzip der Minimierung des Volumens. Dabei spricht man auch dann von einer dichtesten Kugelpackung, wenn die Atome nicht exakt auf den theoretisch vorgegebenen Positionen liegen.

Einatomige Systeme

Kubisch dichteste Kugelpackung (ccp) (links)
Hexagonal dichteste Kugelpackung (hcp) (rechts)

Die Struktur vieler Metalle entspricht einer dichtesten Kugelpackung. Besondere Bedeutung haben dabei die hexagonal dichteste Kugelpackung (hcp) und die kubisch dichteste Kugelpackung (ccp). Insbesondere bei den seltenen Erden gibt es noch einen weiteren Strukturtyp (dhcp).

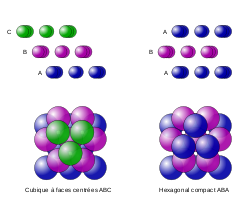
Die hexagonal dichteste Kugelpackung hat die Schichtfolge ABABAB... . Dies führt zur Raumgruppe $\ P6_3 /mmc$. Dieser Strukturtyp hat die Nummer A3 in den Strukturberichten und wird auch Magnesium-Typ genannt. Unter anderem kristallisieren Beryllium, Scandium und Titan in diesem Strukturtyp.

Die kubisch dichteste Kugelpackung hat die Schichtfolge ABCABC... . Dies führt zur Raumgruppe $Fm\bar3m$. Dieser Strukturtyp hat die Nummer A1 in den Strukturberichten und wird auch Kupfer-Typ genannt. Neben Kupfer kristallisieren unter anderem auch Silber und Gold in diesem Strukturtyp.

Insbesondere bei den Seltenen Erden gibt es die Schichtfolge ABCBABCB... . Diese hat dieselbe Raumgruppe, wie die hcp-Struktur, aber mit vier Atomen in der Elementarzelle und zwar auf (0,0,0) / (0,0,1/2) (Wyckoff-Position 2a) und (1/3,2/3,3/4) / (2/3,1/3,1/4) (Wyckoff-Position 2d). Sie wird daher auch double hexagonal closest packed (dhcp) – Struktur genannt. Praseodym ist ein Beispiel für diesen Strukturtyp.

Bei realen Kristallen gibt es oft Abweichungen in der Reihenfolge der Schichten von der Idealstruktur. Dieser Baufehler wird Stapelfehler genannt.

Mehratomige Systeme

Viele Kristallstrukturen mit überwiegend ionischem Bindungstyp beruhen auf einer dichtesten Kugelpackung eines Teils der Ionen und der Einlagerung der anderen Ionen in den Lücken. Sind diese Einlagerungsionen zu groß für die Lücke, wird die Kugelpackung entsprechend deformiert. Die Art und das Ausmaß dieser Deformation hängen dabei von dem Größenverhältnis der Gerüstionen zu den Einlagerungsionen ab. Für einige Stöchiometrien gibt es Beziehungen um aus den Ionenradien sogenannte Toleranzfaktoren zu berechnen. Anhand dieser Toleranzfaktoren kann man Vorhersagen über die Struktur und Verhalten des jeweiligen Systems ableiten. Ein bekanntes Beispiel dafür ist die Perowskit-Struktur.

Polytype

Als Polytype werden Kristalle bezeichnet, die eine Stapelfolge mit langer Wiederholungseinheit besitzen. Beispiele dafür sind Zinksulfid (ZnS) mit mehr als 150 polytypen Formen und Siliciumcarbid (SiC). Diese Polytype verfügen zum Teil über extrem große Gitterkonstanten. So hat das Polytyp von SiC mit der Bezeichnung 393R die Gitterkonstanten a = 3,079 Å und c = 989,6 Å.

Weitere Kugelpackungen

Nicht jede als Strukturtyp vorkommende Kugelpackung ist eine dichteste Kugelpackung. Ein bekanntes Beispiel dafür ist der Strukturtyp A2 (Wolfram-Typ), der auch oft kubisch raumzentriertes Gitter genannt wird (bcc). Diese Kugelpackung hat eine Packungsdichte von ${1 \over 8} \pi \sqrt{3}\approx 0{,}680 \approx 68%$. Unter anderem kristallisieren alle Alkalimetalle in diesem Strukturtyp. Demgegenüber ist der Strukturtyp Ah (α-Polonium), der auch kubisch primitives Gitter (sc) genannt wird, eher selten. Er kommt als Strukturtyp von Hochdruckmodifikationen einiger Elemente vor. Die Packungsdichte beträgt: $\frac{\pi}{6}\approx 0{,}5236\approx 52%$

Weblinks

 Commons: Dichteste Kugelpackung – Sammlung von Bildern, Videos und Audiodateien

• Unterrichtsmaterial zum Thema dichteste Kugelpackung von der IUCr
• Animation einer kubisch dichtesten Kugelpackung
• Anzahl der dichtesten reguläre Kugelpackungen im Raum und Erklärung der Sm-Kristallstruktur
• Darstellung der hexagonalen und kubischen Kugelpackungen

Literatur

• Ch. Kittel: Einführung in die Festkörperphysik. 10. Auflage. Oldenbourg Verlag, München 1993, ISBN 3-486-22716-5.