- Absolut stetig
-
In der Mathematik heißt eine auf einem Intervall I definierte reellwertige Funktion f absolut stetig, falls für jede Zahl
 eine Zahl δ > 0 existiert, welche klein genug ist, so dass für jede (endliche oder unendliche) Folge paarweise disjunkter Intervalle [xk,yk], die in I enthalten sind und der Bedingung
eine Zahl δ > 0 existiert, welche klein genug ist, so dass für jede (endliche oder unendliche) Folge paarweise disjunkter Intervalle [xk,yk], die in I enthalten sind und der Bedingung∑ (yk − xk) < δ k genügen, die folgende Beziehung gilt:
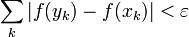 .
.
Jede absolut stetige Funktion ist gleichmäßig stetig und damit insbesondere stetig. Andererseits ist jede Lipschitz-stetige Funktion auch absolut stetig.
Die Cantor-Lebesgue-Funktion ist ein Beispiel für eine überall stetige, aber nicht absolut stetige Funktion.
Absolut stetige Funktionen sind fast überall differenzierbar und diese Ableitung stimmt mit der schwachen Ableitung überein.
Absolute Stetigkeit von Maßen
Sind μ und ν Maße auf der σ-Algebra
 , so bezeichnet man μ als absolut stetig (oder kurz: stetig) bezüglich ν, falls für alle
, so bezeichnet man μ als absolut stetig (oder kurz: stetig) bezüglich ν, falls für alle 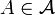 gilt:
gilt: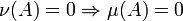 .
.
Man schreibt kurz
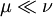 und spricht auch alternativ davon, dass ν das Maß μ dominiert.
und spricht auch alternativ davon, dass ν das Maß μ dominiert.Ein Maß μ auf der reellen Zahlengerade ist genau dann absolut stetig bezüglich des Lebesgue-Maßes auf den Borel-Mengen der reellen Zahlen, wenn für jedes endliche Intervall I die Einschränkung von
auf I eine absolut stetige reelle Funktion ist.
Anwendungsbereiche
- In der Theorie der optimalen Steuerungen wird bislang gefordert, dass die Lösungstrajektorien absolut stetig sind.
- Der Satz von Radon-Nikodym besagt, dass, falls das Maß μ absolut stetig bezüglich eines Maßes ν ist und ν σ-endlich ist, dann μ eine Dichtefunktion, manchmal auch Radon-Nikodym-Ableitung genannt, bezüglich ν besitzt, d.h. es gibt eine messbare Funktion f in
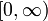 , die wir mit
, die wir mit 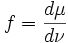 bezeichnen, so dass für jede messbare Menge A gilt:
bezeichnen, so dass für jede messbare Menge A gilt:
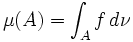 .
.
Dieser Zusammenhang ist in der Wahrscheinlichkeitstheorie von fundamentaler Bedeutung.
Wikimedia Foundation.

![F(x)=\mu((-\infty,x])](/pictures/dewiki/52/4ca81f38935fe50d452987187f20837f.png)