Topologischer Nullteiler

Ein topologischer Nullteiler ist ein Begriff aus der mathematischen Theorie der Banachalgebren. Unter Ausnutzung der Topologie wird der algebraische Begriff des Nullteilers verallgemeinert.

Definition

Sei A eine Banachalgebra über dem Körper der komplexen Zahlen. Ein von 0 verschiedenes Element $x\in A$ heißt linker topologischer Nullteiler, falls es eine Folge (x_n)_n in A gibt mit:

1. $\|x_n\|=1$ für alle n,
2. $x\cdot x_n \xrightarrow{n\to \infty} 0$.

Ein rechter topologischer Nullteiler wird analog definiert, wobei im letzten Punkt natürlich $x_n \cdot x \xrightarrow{n\to \infty} 0$ zu schreiben ist.

Ein beidseitiger oder zweiseitiger topologischer Nullteiler ist ein linker und gleichzeitig rechter topologischer Nullteiler. ^{[1] [2]}

In kommutativen Banachalgebren fallen diese drei Begriffe zusammen und man spricht einfach von topologischen Nullteilern. Manche Autoren lassen auch 0 als topologischen Nullteiler zu; hier liegt also die gleiche uneinheitliche Situation wie bei den algebraischen Nullteilern vor.

Beispiele

• Linke (rechte, zweiseitige) Nullteiler sind linke (rechte, zweiseitige) topologische Nullteiler; man kann in diesem Fall eine konstante Folge (x_n)_n wählen.

Skizze zu den verwendeten Funktionen

• In der Funktionenalgebra C([0,1]) der stetigen Funktionen auf dem Einheitsintervall [0,1] mit der Supremumsnorm ist x = id_[0,1] ein topologischer Nullteiler, der kein Nullteiler ist. x ist kein Nullteiler, denn ist xy = 0, so muss y(t) = 0 zunächst für $0< t \le 1$ gelten, da x auf ]0,1] nicht 0 ist. Die Stetigkeit von y liefert dann für alle $t\in [0,1]$ die Eigenschaft y(t) = 0 und damit muss y = 0 (also die Nullfunktion auf C([0,1])) sein und x ist kein Nullteiler.

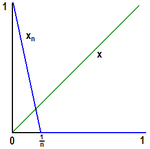
Um zu sehen, dass x ein topologischer Nullteiler ist, betrachte die Funktionen

$x_n(t)=\begin{cases} 1-nt & \mbox{wenn } 0\le t \le \frac{1}{n} \\ 0, & \mbox{sonst} \end{cases}$

Dann ist $\|x_n\|=1$, $\|x\cdot x_n\| = \frac{1}{4n} \rightarrow 0$ und damit x als topologischer Nullteiler nachgewiesen.

• Ist A eine Banachalgebra mit Einselement 1, $x\in A$ kein Vielfaches des Einselements und λ aus dem topologischen Rand des Spektrums von x, so ist $x-\lambda\cdot 1$ ein topologischer Nullteiler. Daraus ergibt sich mit dem Satz von Gelfand-Mazur folgende auf W. Żelasko zurückgehende Aussage: Entweder ist A isomorph zu $\C$ oder A hat topologische Nullteiler.^[3]

Permanent singuläre Elemente

Ein Element einer Banachalgebra A heißt bekanntlich singulär, wenn es nicht invertierbar ist. Ein Element heißt permanent singulär, falls es keine Banachalgebra $\tilde{A}$ gibt mit $A\subset \tilde{A}$ (bzw. A ist isometrisch in $\tilde{A}$ eingebettet), so dass es in $\tilde{A}$ invertierbar ist. Es gilt folgender von R. Arens bewiesener Satz^[4]:

• Ein Element einer kommutativen $\C$-Banachalgebra ist genau dann permanent singulär, wenn es ein topologischer Nullteiler ist.

Nullteiler

Man kann jeden topologischen Nullteiler einer Banachalgebra als echten (algebraischen) Nullteiler einer umfassenden Banachalgebra realisieren. Genauer gilt^[5]:

• Zu jeder Banachalgebra A gibt es eine Banachalgebra $\tilde{A}$, so dass folgendes gilt:

1. A ist isometrisch isomorph zu einer Unterbanachalgebra von $\tilde{A}$.
2. Jeder linke (rechte, zweiseitige) topologische Nullteiler von A ist ein linker (rechter, zweiseitiger) Nullteiler in $\tilde{A}$.

Zur Konstruktion von $\tilde{A}$ sei $\overline{A}$ die Algebra aller beschränkten Folgen in A. Für $(x_n)_n \in \overline{A}$ sei $|(x_n)_n|:= \limsup_{n\to \infty}\|x_n\|$. Dann ist $N:=\{(x_n)_n\in \overline{A};\, |(x_n)_n|=0\}$ ein Ideal in $\overline{A}$ und der Quotient $\tilde{A}=\overline{A}/N$ ist mit der durch $|\cdot |$ induzierten Quotientennorm eine Banachalgebra. Mittels konstanter Folgen kann man A isometrisch isomorph in $\tilde{A}$ einbetten. Ist nun $x\in A$ ein linker topologischer Nullteiler, so gibt es definitionsgemäß eine Folge (x_n)_n in A mit $\limsup_{n\to\infty}\|x\cdot x_n\| = 0$. Daher ist x, aufgefasst als Element in $\tilde{A}$, ein linker Nullteiler.

Einzelnachweise

1. ↑ Wiesław Żelazko: Banach Algebras, Elsevier (1973), ISBN 0-444-40991-2, §14: Topological Divisors of Zero
2. ↑ F. F. Bonsall, J. Duncan: Complete Normed Algebras. Springer-Verlag 1973, ISBN 3-540-06386-2, §1.12
3. ↑ Wiesław Żelazko: Banach Algebras, Elsevier (1973), ISBN 0-444-40991-2, §14.4
4. ↑ Wiesław Żelazko: Banach Algebras, Elsevier (1973), ISBN 0-444-40991-2, §14.7
5. ↑ Wiesław Żelazko: Banach Algebras, Elsevier (1973), ISBN 0-444-40991-2, §14.8