Quotientennorm

Quotientenabbildung ist ein Begriff aus der Funktionalanalysis. Quotientenabbildungen sind lineare Abbildungen, die eine bestimmte Faktorraumstruktur erzeugen.

Definition

Seien X,Y normierte Räume. Eine lineare Abbildung 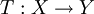$T : X \rightarrow Y$ heißt Quotientenabbildung, wenn sie die offene Einheitskugel 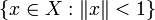$\{x \in X : \|x\| <1 \}$ auf die offene Einheitskugel 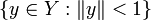$\{y \in Y : \|y\| <1 \}$ abbildet.

Quotientennorm

Es sei 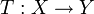$T : X \to Y$ eine Quotientenabbildung. Dann ist T stetig, surjektiv und es gilt 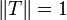$\|T \| = 1$ (falls 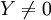$Y \neq 0$). Ferner ist X / ker(T) isometrisch isomorph zu Y.

Ist umgekehrt 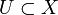$U\subset X$ ein abgeschlossener Unterraum und definiert man auf X / U die Quotientennorm durch 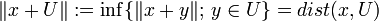$\|x+U\| := \inf\{\|x+y\|;\,y\in U\} = dist(x,U)$, so ist 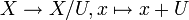$X\rightarrow X/U, x\mapsto x+U$ eine Quotientenabbildung. Die durch die Quotientennorm definierte Topologie stimmt mit der Finaltopologie der Abbildung 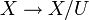$X\rightarrow X/U$ überein. Dieser Zusammenhang rechtfertigt den Namen Quotientenabbildung in obiger Definition.

Eigenschaften

Viele Eigenschaften vererben sich auf die Quotientennorm:

• Ist X ein Banachraum und 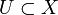$U\subset X$ ein abgeschlossener Unterraum, so ist auch X / U ein Banachraum, d.h. die Vollständigkeit vererbt sich auf die Quotientennorm.
• Ist X ein Hilbertraum und 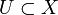$U\subset X$ ein abgeschlossener Unterraum, so ist auch X / U ein Hilbertraum, d.h. auch die Quotientennorm wird durch ein Skalarprodukt erzeugt.
• Ist X ein gleichmäßig konvexer Raum und 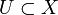$U\subset X$ ein abgeschlossener Unterraum, so ist auch X / U gleichmäßig konvex.
• Ist X eine Banachalgebra und 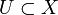$U\subset X$ ein abgeschlossenes zweiseitiges Ideal, so ist auch X / U eine Banachalgebra, d.h. die Submultiplikativität der Norm überträgt sich auf die Quotientennorm.
• Ist X eine C^*-Algebra und 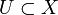$U\subset X$ ein abgeschlossenes zweiseitiges Ideal, so ist auch X / U eine C^*-Algebra, d.h. die C^*-Eigenschaft der Norm gilt auch für die Quotientennorm.

Lokalkonvexe Räume

Die Topologie eines lokalkonvexen Raumes X wird durch eine Menge 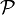$\mathcal P$ von Halbnormen erzeugt. Sei 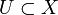$U\subset X$ ein Unterraum. Für jedes 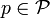$p\in \mathcal P$ ist die Quotientenhalbnorm 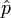$\hat{p}$ eine Halbnorm auf dem Quotientenraum X / U, wobei 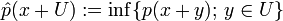$\hat{p}(x+U) := \inf\{p(x+y);\,y\in U\}$. Dann stimmt die Finaltopologie auf X / U mit der durch die Halbnormen 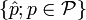$\{\hat{p};p\in {\mathcal P}\}$ erzeugten Topologie überein, insbesondere ist der Quotientenraum wieder lokalkonvex.

Siehe auch

• Homomorphiesatz
• Faktorraum

Literatur

• Dirk Werner: Funktionalanalysis. Springer-Verlag, 2004