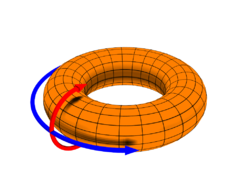
Toroidale-Poloidale Zerlegung

In diesem Diagramm wird die poloidale Richtung (θ) in rot angezeigt. Die toroidale Richtung (ζ oder ϕ) ist blau dargestellt.

Die Toroidale-Poloidale Zerlegung unterteilt ein Magnetfeld, z. B. das Erdmagnetfeld, in zwei Anteile, die jeweils nur von einem Skalarfeld abhängen. Die Zerlegung geht von einem Vektorpotential A des Magnetfelds B aus. Es lässt sich in eine radiale A_r und eine tangentiale Komponente A_t aufteilen.

$\mathbf{A} = \mathbf{A_r} + \mathbf{A_t} = \Psi \mathbf{r} + \mathbf{r} \times A_2$

Durch geeignete Wahl des poloidalen Vektorpotentials A₂ lässt es sich aus einem Divergenzfeld ableiten, ohne dass das Magnetfeld geändert wird.

$A_2 := \nabla \chi$

Toroidales Feld

Das toroidale Feld B_t ergibt sich aus der Rotation des Vektorpotentials $\mathbf{A_r}$:

$B_{t} = \operatorname{rot} \mathbf{A_r} = \operatorname{rot} \Psi \mathbf{r}.$

Durch Ausmultiplizieren der Rotation in Kugelkoordinaten sieht man, dass das Feld keine radialen Anteile hat:

$B_{t} = \operatorname{rot} \mathbf{A_r} = \frac{1}{\sin \theta}\frac{\partial \Psi}{\partial \varphi} \mathbf e_\theta - \frac{\partial \Psi}{\partial \theta} \mathbf e_\varphi$

Das Feld ist auf der Kugeloberfläche divergenzfrei. Anschaulich bedeutet das, dass das Feld keine Quellen und Senken hat. Andererseits gibt es keinen radialen Feldfluss. Ein toroidales Magnetfeld kann damit nur innerhalb von Materie von Null verschieden sein. Das bedeutet in der Geophysik, dass vom Erdkern erzeugte toroidale Felder an der Oberfläche nicht gemessen werden können. ^[1]

Der Begriff toroidal leitet sich aus der Torusform dieser Felder in rotationssymmetrischen Systemen ab. Für die Beschreibung allgemeiner toroidaler Felder ist er daher missverständlich.

Poloidales Feld

Das poloidale Feld B_p entsteht aus der Rotation des Vektorpotentials $\mathbf{A_t}$.

$B_{p} = \operatorname{rot} \mathbf{A_t} = \operatorname{rot} (\mathbf{r} \times \nabla \chi)$

Es hat sowohl radiale als auch tangentiale Komponenten. Der Begriff leitet sich aus der Dipol-Form beim Erdmagnetfeld ab. Da das toroidale Feld nur in Materie auftritt, beschreibt das poloidale Feld das Erdmagnetfeld oberhalb der Erdoberfläche vollständig.

Beispiele

zentraler Dipol

Das Feld eines magnetischen Dipols im Koordinatenursprung hat ein Vektorpotential

$\vec{A}(\vec{r})\,=\,\frac{\mu_0}{4 \pi}\,\frac{\vec{m}\times\vec{r}}{r^3}$ ,

welches sofort als poloidales Feld erkennbar ist. Das damit verbundene Potential χ ergibt sich aus der Multipolentwicklung zu

$\chi(\vec{r}) = \frac{\mu_0}{4 \pi}\,\frac{\vec{m} \vec{r}}{r^3}$.

Falls sich Dipole außerhalb des Koordinatenursprungs befinden, so enthält das Feld auch Multipolmomente anderer Ordnungen.

radialer Dipol

Wenn der zuvor beschriebene radiale Dipol entlang des magnetischen Moments verschoben wird (d.h. das magnetische Moment liegt in Radialrichtung), so ändert sich das Vektorpotential in

$\vec{A_t}(\vec{r})\,=\,\frac{\mu_0}{4 \pi}\,\frac{\vec{m}\times(\vec{r}- \vec{c_m})}{|\vec{r}-\vec{c_m}|^3} \,=\,\frac{\mu_0}{4 \pi}\,\frac{\vec{m}\times \vec{r}}{|\vec{r}-\vec{c_m}|^3}$.

Das zugehörige Potential χ ist

$\chi(\vec{r}) = \frac{\mu_0}{4 \pi}\,\frac{\vec{m} (\vec{r}- \vec{c_m})}{|\vec{r}-\vec{c_m}|^3}$.

tangentialer Dipol

Das bedeutet, dass aus radialen Dipolmomenten ausschließlich ein poloidales Feld erzeugt werden kann. Für die Erzeugung toroidaler Komponenten müssen tangentiale magnetische Momente beteiligt sein.

$\vec{A}(\vec{r})\,=\,\frac{\mu_0}{4 \pi}\,\frac{\vec{m}\times(\vec{r}- \vec{c_{\perp m}})}{|\vec{r}-\vec{c_{\perp m}}|^3} \,=\, \frac{\mu_0}{4 \pi}\,\frac{\vec{m}\times \vec{r}-(\vec{m}\times \vec{c_{\perp m}} - ((\vec m \times \vec {c_{\perp m}})\vec{e_r})\vec{e_r}) }{|\vec{r}-\vec{c_{\perp m}}|^3} - \frac{\mu_0}{4 \pi} \frac{((\vec m \times \vec {c_{\perp m}})\vec{e_r})\vec{e_r}}{|\vec{r}-\vec{c_{\perp m}}|^3}$.

Der erste Summand stellt den poloidalen Teil des Feldes dar, der zweite den toroidalen Anteil.

$\vec{A_t}(\vec{r})\,=\,- \frac{\mu_0}{4 \pi} \frac{((\vec m \times \vec {c_{\perp m}})\vec{e_r})\vec{e_r}}{|\vec{r}-\vec{c_{\perp m}}|^3}$

Legt man das magnetische Moment auf die Z-Achse und den Dipol selbst auf die X-Achse, so erhält man

$B_{t} = \operatorname{rot} \mathbf{A_r} = \operatorname{rot} \Psi \mathbf{r} = \frac{\mu_0 m c_{\perp m}}{4 \pi}\operatorname{rot} \frac{y}{r^2|\vec{r}-\vec{c_{\perp m}}|^3} \vec{r}$

Radiale und tangentiale Dipole können als Basis zum Aufbau des Magnetfeldes dienen. D.h. zusammen mit räumlichen Drehungen der Basiselemente lässt sich jede magnetische Konfiguration erstellen. Wenn man also für beide Dipole Potentiale ψ und χ bestimmt, kann man für jede Konfiguration die Gesamtpotentiale errechnen.

Anwendung

• Toroidale Felder werden in Kernfusionsanlagen für den Einschluss des Fusionsplasmas verwendet.
• In der Geo- oder Heliodynamik finden poloidale und toroidale Felder Anwendung bei der Berechnung des Magnetfelds des Erdkerns und der Sonne.

Literatur

• Eric W. Weisstein: Toroidal Field. In: MathWorld. (englisch)
• Eric W. Weisstein: Poloidal Field. In: MathWorld. (englisch)
• Eric W. Weisstein: Divergenceless Field. In: MathWorld. (englisch)
• toroidal field (englisch)
• Übungsblatt der Uni-München

Einzelnachweise

1. ↑ Jan Dostal: Prädikation ozeanischer Tidensignale in Satellitenbeobachtungen des Erdmagnetfeldes S.21ff ISSN 1610-0956

Siehe auch

• Vektorfeld