Rational elliptische Funktionen

Darstellung der rational elliptischen Funktionen zwischen x=-1 und x=1 für die Ordnungen 1,2,3 und 4 mit dem Selektivfaktor ξ=1,1.

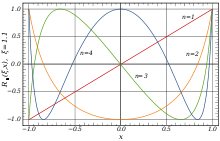
Die Rational elliptische Funktionen stellen in der Mathematik eine Reihe von rationalen Funktionen mit reellen Faktoren dar. Sie werden zum Entwurf von Übertragungsfunktionen bei Cauer-Filtern in der elektronischen Signalverarbeitung verwendet.

Eine bestimmte rational elliptische Funktion wird durch ihre Ordnung n und einem reellen Selektivfaktor ξ ≥ 1 charakterisiert. Formal sind die rational elliptischen Funktionen mit dem Parameter x definiert als:

$R_n(\xi,x)\equiv \mathrm{cd}\left(n\frac{K(1/L_n)}{K(1/\xi)}\,\mathrm{cd}^{-1}(x,1/\xi),1/L_n\right)$

wobei die Funktion cd(·) eine abgeleitete jacobische elliptische Funktion, bestehend aus den cosinus amplitudinis und den delta amplitudinis darstellt. K(·) steht für das elliptische Integral erster Art und L_n(ξ) = R_n(ξ,ξ) stellt einen Diskriminierungsfaktor dar, welcher für $|x|\ge\xi$ gleich dem kleinsten Betragswert von R_n(ξ,x) ist.

Ausdruck als rationale Funktion

Für Ordnungen in der Form n=2^a3^b, mit a und b positiv ganzzahlig, können die rational elliptische Funktionen durch analytische Funktionen ausgedrückt werden.

Für gerade Ordnung n können die rational elliptischen Funktionen in diesen Fällen als Quotient zweier Polynome, beide mit Ordnung n, ausgedrückt werden als:

$R_n(\xi,x)=r_0\,\frac{\prod_{i=1}^n (x-x_i)}{\prod_{i=1}^n (x-x_{pi})}$      (n gerade)

mit den Nullstellen x_i und den Polstellen x_pi. Der Faktor r₀ wird so gewählt, dass R_n(ξ,1) = 1 gilt.

Für ungerade Ordnung ergibt sich ein Pol bei x=∞ und eine Nullstelle bei x=0, womit rational elliptischen Funktionen bei ungerader Ordnung in der Form

$R_n(\xi,x)=r_0\,x\,\frac{\prod_{i=1}^{n-1} (x-x_i)}{\prod_{i=1}^{n-1} (x-x_{pi})}$      (n ungerade)

ausgedrückt werden können.

Damit lassen sich die ersten Ordnungen der rational elliptische Funktionen formulieren:

R₁(ξ,x) = x

$R_2(\xi,x)=\frac{(t+1)x^2-1}{(t-1)x^2+1}$, mit $t \equiv \sqrt{1-\frac{1}{\xi^2}}$.

$R_3(\xi,x)=x\,\frac{(1-x_p^2)(x^2-x_z^2)}{(1-x_z^2)(x^2-x_p^2)}$, mit $G\equiv\sqrt{4\xi^2+(4\xi^2(\xi^2\!-\!1))^{2/3}}$, $x_p^2\equiv\frac{2\xi^2\sqrt{G}}{\sqrt{8\xi^2(\xi^2\!+\!1)+12G\xi^2-G^3}-\sqrt{G^3}}$, $x_z^2=\xi^2/x_p^2$

Weitere Ordnungen lassen sich dann mittels niedriger Ordnungen mittels der Verschachtelungseigenschaft bilden:

$R_4(\xi,x)=R_2(R_2(\xi,\xi),R_2(\xi,x))=\frac{(1+t)(1+\sqrt{t})^2x^4-2(1+t)(1+\sqrt{t})x^2+1}{(1+t)(1-\sqrt{t})^2x^4-2(1+t)(1-\sqrt{t})x^2+1}$

R₅(ξ,x), keine rationale Funktion.

$R_6(\xi,x)=R_3(R_2(\xi,\xi),R_2(\xi,x))\,$

Eigenschaften

Normalisierung

Alle rational elliptische Funktionen sind bei x=1 auf 1 normiert:

R_n(ξ,1) = 1

Verschachtelung

Bei der Eigenschaft der Verschachtelung gilt:

$R_m(R_n(\xi,\xi),R_n(\xi,x))=R_{m\cdot n}(\xi,x)$

Aus der Eigenschaft zur Verschachtelung folgt unmittelbar die obige Regel zur Angabe von bestimmten Ordnungen als rationale Funktion, da sich R₂ und R₃ als geschlossener analytischer Ausdruck angeben lassen. Damit lassen sich alle Ordnungen n=2^a3^b in Form von analystischen Funktionen angeben.

Grenzwerte

Die Grenzwerte der rational elliptische Funktionen für ξ→∞ lassen sich als Tschebyschow-Polynome erster Art T_n ausdrücken:

$\lim_{\xi=\rightarrow\,\infty}R_n(\xi,x) = T_n(x)$

Symmetrie

Es gilt allgemein:

R_n(ξ, − x) = R_n(ξ,x) für gerade n

$R_n(\xi,-x)=-R_n(\xi,x)\,$ für ungerades n

Welligkeit

R_n(ξ,x) hat eine einheitliche Welligkeit von ±1 im Intervall -1≤x≤1.

Kehrwert

Es gilt allgemein:

$R_n(\xi,\xi/x)=\frac{R_n(\xi,\xi)}{R_n(\xi,x)}$

Die bedeutet, dass die Pole und Nullstellen paarweise auftreten müssen und der Beziehung:

$x_{pi}x_{zi}=\xi\,$

genügen müssen. Ungerade Ordnungen weisen somit eine Nullestelle bei x=0 und eine Polstelle bei Unendlich auf.

Quellen

• Elliptic rational functions auf MathWorld (engl.)

Literatur

• Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. 2. Auflage. Springer, 2007, ISBN 978-3-540-49324-2.