Chow-Test

Der Chow-Test ist ein statistischer Test, mit dem sich die Koeffizienten zweier linearer Regressionen auf Gleichheit testen lassen. Der Test ist nach seinem Erfinder, dem Ökonomen Gregory Chow, benannt.

Der Chow-Test wird in der Ökonometrie verwendet, um Zeitreihen auf Strukturbrüche zu testen. Ein weiteres Anwendungsgebiet ist die Programmevaluation, hierbei werden zwei unterschiedliche Teilgruppen (Programme), wie zum Beispiel zwei Schultypen, miteinander verglichen. Im Gegensatz zur Zeitreihenanalyse lassen sich hier die beiden Teilgruppen keinen aufeinander folgenden Intervallen zuordnen, stattdessen erfolgt die Einteilung nach einem qualitativen Aspekt, wie zum Beispiel dem Schultyp.

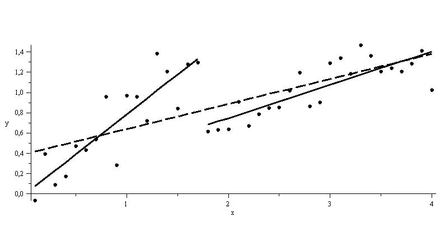
Strukturbruch	Programmevaluation
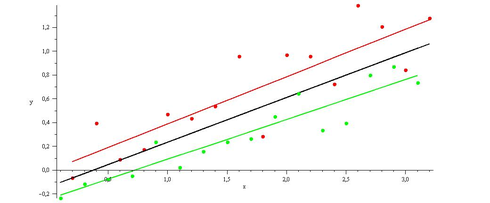
Bei x = 1.7 liegt ein Strukturbruch vor, Regressionen auf den Teilintervallen [0,1.7] und [1.7,4] liefern eine bessere Modellierung als die Regression über dem Gesamtinterval (gestrichelt)	Vergleich zweier Programme (rot, grün) im selben Datensatz, separate Regressionen auf den zu einem Programm gehörigen Daten liefern eine bessere Modellierung als die Regression über den gesamten Datensatz (schwarz)

Vorgehen

Gegeben ist ein Datensatz (Y_i,X_i) mit $X_i=(x_{i1},\ldots,x_{ik})$ für $i=1\ldots N$, dessen Beziehung durch eine lineare Funktion mit einem normalverteilten Fehler (ε) mit Erwartungswert 0 ($E(\epsilon)=0$) beschrieben wird (multiple Regressionsanalyse), d.h. man hat

$Y_{i}=c_0+c_1x_{i1}+c_2x_{i2}+\ldots+c_kx_{ik}+\epsilon_i$ für $i=1\ldots N$.

Man vermutet jedoch, dass sich der Datensatz in zwei Gruppen aufteilen lässt, die durch zwei unterschiedliche lineare Funktionen besser beschrieben werden.

$Y_{i}=a_0+a_1x_{i1}+a_2x_{i2}+\ldots+a_kx_{ik}+\epsilon_i$ für $i=1\ldots N_a$

$Y_{i}=b_0+b_1x_{i1}+b_2x_{i2}+\ldots+b_kx_{ik}+\epsilon_i$ für $i=N_a+1\ldots N$

Hierbei ist N = N_a + N_b und es wird die Hypothese $H_0:\, (a_0,a_1,\ldots,a_k)=(b_0,b_1,\ldots,b_k)$ gegen $H_1:\, (a_0,a_1,\ldots,a_k)\neq (b_0,b_1,\ldots,b_k)$ getestet. Bezeichnet man die Summe der quadrierten Residuen der Regression über den gesamten Datensatz mit S und über die beiden Teilgruppen mit S_a und S_b, dann folgt die unten definierte Testgröße T einer F-Verteilung mit den Freiheitsgraden k + 1 und N_a + N_b − 2(k + 1).

$T:=\frac{(S-(S_a+S_b))/(k+1)}{(S_a+S_b)/(N_a+N_b-2(k+1))}$

Beispiel

Gegeben ist der folgende Datensatz, dessen Beziehung durch die lineare Funktion Y = c₀ + c₁X modelliert werden soll:

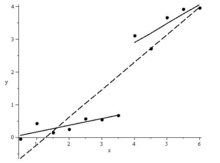
Xi	0,5	1,0	1,5	2,0	2,5	3,0	3,5	4,0	4,5	5,0	5,5	6,0
Yi	−0,043	0,435	0,149	0,252	0,571	0,555	0,678	3,119	2,715	3,671	3,928	3,962

Der Datenplot legt einen Strukturbruch bei x = 4 nahe.

Ein Datenplot lässt vermuten, dass bei x = 4 ein Strukturbruch vorliegt, daher teilt man den Datensatz in 2 Intervalle [0.5,3.5] und [4.0,6.0] ein und führt über diesen, zusätzlich zur Regression über den gesamten Datensatz, getrennte Regressionen durch. Dann testet man, ob die beiden Teilregressionen dieselbe lineare Funktion erzeugen, also $H_0:\,(a_0,a_1)=(b_0,b_1)$ gegen $H_1:\,(a_0,a_1)\neq(b_0,b_1)$

Regression auf dem gesamten Datensatz:

$\overline{x}=\frac{1}{12}\sum_{i=1}^{12} X_i=3.250$	$\overline{y}=\frac{1}{12}\sum_{i=1}^{12} Y_i= 1.666$
$S_{xx}=\sum_{i=1}^{12} (X_i-\overline{x})^2=37.750$	$S_{yy}=\sum_{i=1}^{12} (Y_i-\overline{y})^2= 29.771$
$S_{xy}=\sum_{i=1}^{12} (X_i-\overline{x})(Y_i-\overline{y})=30.061$	$S=S_{yy}-\frac{S_{xy}^2}{S_{xx}}=4.933$

Regression auf [0.5,3.5]

$\overline{x}=\frac{1}{7}\sum_{i=1}^{7} X_i=2.000$	$\overline{y}=\frac{1}{7}\sum_{i=1}^{7} Y_i= 0.371$
$S_{xx}=\sum_{i=1}^{7} (X_i-\overline{x})^2=7.000$	$S_{yy}=\sum_{i=1}^{7} (Y_i-\overline{y})^2= 0.408$
$S_{xy}=\sum_{i=1}^{7} (X_i-\overline{x})(Y_i-\overline{y})=1.415$	$S_a=S_{yy}-\frac{S_{xy}^2}{S_{xx}}=0.122$

Datenplot mit Regressionsgeraden.

Regression auf [4.0,6.0]

$\overline{x}=\frac{1}{5}\sum_{i=1}^{5} X_i=5.000$	$\overline{y}=\frac{1}{5}\sum_{i=1}^{5} Y_i= 4.800$
$S_{xx}=\sum_{i=1}^{5} (X_i-\overline{x})^2=2.500$	$S_{yy}=\sum_{i=1}^{5} (Y_i-\overline{y})^2= 1.186$
$S_{xy}=\sum_{i=1}^{5} (X_i-\overline{x})(Y_i-\overline{y})=1.450$	$S_b=S_{yy}-\frac{S_{xy}^2}{S_{xx}}=0.345$

Berechnung der Testgröße:

$T:=\frac{(S-(S_a+S_b))/(k+1)}{(S_a+S_b)/(N_a+N_b-2(k+1))}=34.484$

Wegen $F_{2;8;0,95}=4,459\,$  (Signifikanzniveau $\alpha = 0,05\,$) gilt  $T\ge F_{2;8;0,95}$. Somit kann die Nullhypothese $H_0\,$ verworfen werden. Das heißt, die beiden Regressionsgeraden auf den Teilintervallen sind nicht identisch. Es liegt also ein Strukturbruch vor und die Teilregressionen liefern eine bessere Modellierung als die Regression über den gesamten Datensatz.

Literatur

• Howard E. Doran: Applied Regression Analysis in Econometrics. CRC Press 1989, ISBN 0-8247-8049-3, S.146 (eingeschränkte Online-Version (Google Books))
• Christopher Dougherty: Introduction to Econometrics. Oxford University Press 2007, ISBN 0-19-928096-7, S.194 (eingeschränkte Online-Version (Google Books))
• Gregory C. Chow: Tests of Equality Between Sets of Coefficients in Two Linear Regressions. In: Econometrica. 28(3), 1960, S. 591–605.