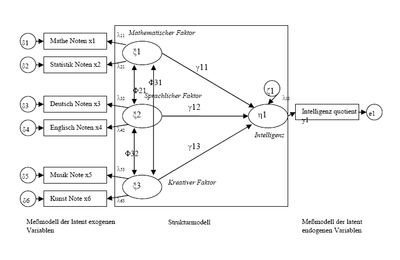
Strukturgleichungsmodell

Der Begriff Strukturgleichungsmodell bezeichnet ein statistisches Verfahren zum Testen und Schätzen auch kausaler Zusammenhänge. Dabei kann überprüft werden, ob die vor der Anwendung des Verfahrens angenommenen Hypothesen mit den gegebenen Variablen übereinstimmen. Es wird den strukturprüfenden multivariaten Verfahren zugerechnet und besitzt einen konfirmatorischen (bestätigenden) Charakter.

Strukturgleichungsmodelle spielen unter anderem in der empirischen Sozialforschung eine wichtige Rolle. Eine Besonderheit von Strukturgleichungsmodellen ist das Überprüfen latenter (nicht direkt beobachtbarer) Variablen. Pfadanalyse, Faktoranalyse und Regressionsanalyse können als Spezialfälle von Strukturgleichungsmodellen angesehen werden.^[1] Ein Strukturgleichungsmodell stellt wiederum einen Spezialfall eines Kausalmodells dar.^[2]

Modellelemente

Strukturgleichungsmodell mit der latenten Variable „Intelligenz“

• Indikator (Item): Hierbei handelt es sich um beobachtete Variablen. Beispielsweise sind Indikatoren für „Intelligenz“ die „Abschlussnote im Abitur“, der „Intelligenzquotient“ und die „Anzahl der Sprachen, die eine Person beherrscht“. Üblicherweise wird im Modell die Verwendung von mindestens vier Indikatoren empfohlen.
• Latente Variable (Faktor): Hierbei handelt es sich um die unbeobachtete Variable, die erst durch ihre Indikatoren gemessen wird. Im Beispiel ist „Intelligenz“ die latente Variable. Es wird zwischen unabhängigen latenten (= exogenen) und abhängig latenten (= endogenen) Variablen unterschieden.
• Messmodell (measurement model): Hierbei handelt es sich um den Kern des Strukturgleichungsmodells. In ihm werden im Sinne einer konfirmatorischen Faktorenanalyse (confirmatory factor analysis) Verbindungen zwischen den Indikatoren und den latenten Variablen modelliert. Hierbei spielt die Kovarianz eine entscheidende Rolle.
• Strukturmodell (structural model): Hierbei handelt es sich um die Menge exogener und endogener Variablen und deren Verbindungen.

Modellierung

Für die Modellierung haben Mulaik und Millsap (2000) vier Schritte vorgeschlagen.^[3] Im ersten Schritt wird eine Faktorenanalyse durchgeführt, um die Anzahl der latenten Variablen zu bestimmen. Mit einer konfirmatorischen Faktorenanalyse wird im zweiten Schritt das Messmodell bestätigt. Im dritten Schritt wird das Strukturmodell getestet. Im vierten Schritt werden verschachtelte Modelle getestet, um die sparsamsten zu identifizieren.

Allerdings ist zu beachten, dass in der Literatur davor gewarnt wird, Modelle so lange zu modifizieren bis sie "passen". Vielmehr muss zur Überprüfung veränderter bzw. neuer Hypothesen immer eine neue Stichprobe erhoben werden^[4][5].

Software

Zur Erstellung von Strukturgleichungsmodellen haben sich die Software-Pakete LISREL, AMOS und EQS etabliert, wobei AMOS als Erweiterung von SPSS dient. AMOS gilt als benutzerfreundlicher als das ältere, jedoch nach wie vor etablierte LISREL.^[6]

Die Statistik-Software R unterstützt die Erstellung von Strukturgleichungsmodellen z.B. mit dem Paket sem^[7].

Die kommandozeilenbasierte Software Mplus von Muthén & Muthén ermöglicht explizit die Berücksichtigung von Gewichtungsfaktoren, wie sie beispielsweise im Rahmen von Panelerhebungen Verwendung finden.

Weiterhin erfreuen sich Softwarepakete, die auf dem Partial Least Squares (PLS) Verfahren basieren, wie SmartPLS, PLSGraph, ProPLS, etc. in Forschung und Praxis wachsender Beliebtheit ^[8]

Literatur

• B.M. Byrne: Structural Equation Modeling with EQS and EQS/Windows. Basic Concepts, Applications, and Programming. Thousand Oaks. 1994.
• Weiber/Mühlhaus (2009): Strukturgleichungsmodellierung: Eine anwendungsorientierte Einführung in die Kausalanalyse mit Hilfe von AMOS, SmartPLS und SPSS. Springer. ISBN 3642028764

Weblinks

• Strukturgleichungsmodelle. TeachWiki-Seite mit praktischem Beispiel und näheren mathematischen Details.
• Online-Kurs der FU Berlin
• Handbook of Management Scales, enthält eine Reihe von Skalen zur Messung von Konstrukten, die in Strukturgleichungsmodellen der betriebswirtschaftlichen Forschung verwendet werden können.

Einzelnachweise

1. ↑ Klaus Backhaus, Wulff Plinke, Bernd Erichson, Rolf Weiber: Multivariate Analysemethoden — eine anwendungsorientierte Einführung. 11 Auflage. Springer, Berlin/Heidelberg 2006, ISBN 9783540299325.
2. ↑ Ronald D. Anderson, Gyula Vastag: Causal modeling alternatives in operations research: Overview and application. In: European Journal of Operational Research. Vol. 156, 2004, S. 92-109 (PDF, abgerufen am 18. Oktober 2011).
3. ↑ Stanley A. Mulaik, Roger E. Millsap: Doing the four-step right. In: Structural Equation Modeling. Vol. 7, Nr. 1, 2000, S. 36-73, doi:10.1207/S15328007SEM0701_02.
4. ↑ Klaus Backhaus, Bernd Erichson, Wulff Plinke, Rolf Weiber: Multivariate Analysemethoden — Eine anwendungsorientierte Einführung. 12 Auflage. Springer/Heidelberg, Berlin 2008, ISBN 978-3-540-85044-1.
5. ↑ Jürgen Bortz, René Weber: Statistik. 6 Auflage. Springer, Heidelberg 2005, ISBN 3-540-21271-X, doi:10.1007/b137571.
6. ↑ R. B. Kline: Software Review: Software programs for structural equation modeling: AMOS, EQS, and LISREL. In: Journal of Psychoeducational Assessment. Vol. 16, Nr. 4, 1998, S. 343-364, doi:10.1177/073428299801600407.
7. ↑ John Fox: Teacher's Corner: Structural-Equation Modeling with the sem Package in R. In: Structural Equation Modeling. Vol. 13, Nr. 3, 2006, S. 465-486 (PDF, abgerufen am 18. Oktober 2011).
8. ↑ Rolf Weiber, Daniel Mühlhaus: Strukturgleichungsmodellierung: Eine anwendungsorientierte Einführung in die Kausalanalyse mit Hilfe von AMOS, SmartPLS und SPSS. 1 Auflage. Springer, Berlin/Heidelberg 2009, ISBN 978-3642028762.