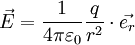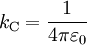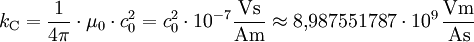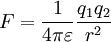Coulombisches Gesetz

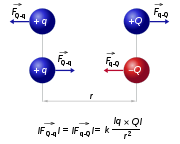
Das Coulombsche Gesetz (nach Charles Augustin de Coulomb, 1785) bildet die Basis der Elektrostatik und beschreibt die Kraft zwischen zwei kugelsymmetrisch verteilten elektrischen Ladungen. Es besagt, dass der Betrag dieser Kraft proportional zum Produkt der beiden Ladungsmengen und umgekehrt proportional zum Quadrat des Abstandes der Kugelmittelpunkte ist. Die Kraft wirkt je nach Vorzeichen der Ladungen anziehend oder abstoßend in Richtung der Verbindungsgeraden der Mittelpunkte. Bei mehr als zwei Ladungen werden die einzelnen Kraftvektoren addiert (Superposition).

Das Coulombsche Gesetz ist Grundlage der Influenz.

Coulomb-Kraft

Grundmechanismus: Ladungen mit gleichem Vorzeichen stößen sich ab, Ladungen mit mit unterschiedlichen Vorzeichen ziehen sich an.

Torsionspendel von Coulomb mit dem er Kraftmessungen durchführte

Das Coulombsche Gesetz wurde von Coulomb um 1785 entdeckt und in umfangreichen Experimenten bestätigt. Im Internationalen Einheitensystem und in skalarer Form ist die Kraft demnach

$F = \frac{1}{4\pi\varepsilon_0} \frac{q_1 \cdot q_2}{r^2}$,

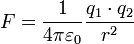wobei q₁ und q₂ zwei jeweils kugelsymmetrisch verteilte Ladungsmengen, r der Abstand zwischen deren Mittelpunkten und 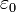$\varepsilon_0$ die Permittivität des Vakuums (elektrische Feldkonstante) sind. Die allgemeine vektorielle Notation ergibt das Coulomb-Kraftfeld:

$\vec{F} = \frac{1}{4\pi\varepsilon_0} \frac{q_1 \cdot q_2}{r^2} \cdot \vec{e_r}$.

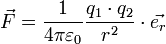Hierbei ist 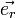$\vec{e_r}$ ein Einheitsvektor in Richtung der Verbindungslinie der Ladungsmittelpunkte. Dabei gilt, dass sich Ladungen mit gleichem Vorzeichen (gleichnamige Ladungen) abstoßen und solche mit verschiedenem Vorzeichen (ungleichnamige Ladungen) anziehen.

Weiter ist

$\vec{E} = \frac{1}{4\pi\varepsilon_0}\frac{q}{r^2} \cdot \vec{e_r}$

der Vektor der Feldstärke des von der Ladung q erzeugten elektrischen Feldes im Abstand r vom Mittelpunkt.

Die Konstante

$k_\mathrm{C} = \frac {1}{4 \pi \varepsilon_0}$

wird auch als Coulomb-Konstante bezeichnet. Es gilt:

$k_\mathrm{C} = \frac {1}{4 \pi} \cdot \mu_0 \cdot c_0^2 = c_0^2 \cdot 10^{-7} \mathrm{\frac{Vs}{Am}} \approx 8{,}987551787 \cdot 10^9 \, \mathrm{\frac{Vm}{As}}$

Im Gaußschen und elektrostatischen CGS-Einheitensystem wird das Coulombsche Gesetz zur Definition der elektrischen Ladung benutzt. Eine Ladungseinheit wirkt auf eine zweite im Abstand 1 cm mit der Kraft 1 dyn. Die elektrische Basiseinheit der Einheitensysteme SI, CGS-ESU und CGS-EMU unterscheidet sich prinzipiell nur durch die Festlegung von μ₀:

• Im CGS-ESU ist μ₀ auf 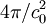$4\pi/c_0^2$ festgelegt. Daher ist die Coulomb-Konstante eine dimensionslose Größe mit dem Wert 1.

• Im CGS-EMU ist μ₀ auf die dimensionslose Größe von 4π festgelegt. Daher ist die Coulomb-Konstante gleich $c_0^2$.

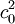Coulomb-Kraft in einem Medium

Das Coulombsche Gesetz lässt sich auf einfache Weise auf den Fall von Ladungen in homogenen, isotropen, linearen Medien erweitern. Das die Ladungen umgebende Material muss sich dazu in guter Näherung diese Eigenschaften besitzen:

• Es ist elektrisch neutral.
• Es füllt den Raum zwischen den Ladungen und um diese herum gleichmäßig (homogen) aus.
• Die Polarisierbarkeit des Mediums ist richtungsunabhängig.
• Die Polarisierung ist proportional zum elektrischen Feld, das von den Ladungen erzeugt wird.

Insbesondere verlangt die Homogenität, dass der atomare Charakter der Materie im Vergleich zum Abstand der Ladungen vernachlässigbar ist.

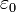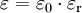Für solche Medien schreibt sich das Coulombsche Gesetz in gleicher Form wie im Vakuum, mit dem einzigen Unterschied, dass $\varepsilon_0$ durch $\varepsilon = \varepsilon_0\cdot\varepsilon_\mathrm{r}$ ersetzt wird.

$F = \frac{1}{4\pi\varepsilon} \frac{q_1 q_2}{r^2}$

Die relative Permittivität 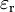$\varepsilon_\mathrm{r}$ ist bei isotropen Medien eine Materialkonstante, die der Polarisierbarkeit des Mediums Rechnung trägt. Sie kann sowohl durch Messungen als auch aus theoretischen Überlegungen gewonnen werden.

In der Umkehrung gilt im Vakuum $\varepsilon_\mathrm{r}=1$.

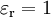Literatur

• Dieter Meschede: Gerthsen Physik. 23. Auflage, Springer, Berlin/Heidelberg/New York 2006, ISBN 3-540-25421-8