De re und de dicto

Mit den Bezeichnungen de dicto und de re (lat. „über das Gesagte“ und „über die Sache“) beschreibt man in der Logik und Sprachphilosophie einen Bedeutungsunterschied bei intensionalen Operatoren wie den Modalbegriffen möglich und notwendig. Im Fall einer Modalität „de dicto“ resultiert die Notwendigkeit aus der Art und Weise, wie eine bestimmte Sache beschrieben wird, im Falle einer Modalität „de re“ in der Sache selbst.

Zur Erläuterung betrachte man folgendes Beispiel:

Junggesellen sind notwendig unverheiratet.

Die hier ausgedrückte Notwendigkeit liegt in sprachlichen Tatsachen begründet, ist also eine Modalität de dicto: Der Begriff des Junggesellen impliziert das Unverheiratet-Sein. Wenn wir eine bestimmte Person also als Junggesellen beschreiben, so folgt notwendig daraus, dass die Person unverheiratet ist. Diese Eigenschaft hat die Person aber nicht unabhängig von der Beschreibung als Junggeselle, es liegt kein Widerspruch in der Annahme, dass die Person irgendwann heiratet.

Für ein Beispiel einer Modalaussage de re betrachten wir folgenden Satz, ausgesagt von einem bestimmten Menschen Frank:

Frank ist notwendig ein Lebewesen.

Die hier ausgesagte Notwendigkeit liegt nicht in der Art und Weise, wie Frank beschrieben wird (tatsächlich wird er ja auch nur mit seinem Namen bezeichnet), sondern in der Sache selbst begründet: Frank könnte seine Eigenschaft, ein Lebewesen zu sein, nicht verlieren, ohne dabei aufzuhören, Frank zu sein. Insofern bezeichnet man Franks Lebewesen-Sein auch als „essentielle“ oder „wesentliche“ Eigenschaft, als Essenz von Frank.

Den Unterschied zwischen der de-dicto- und der de-re-Lesart kann man in der formalen Modallogik durch die Position und damit Reichweite des Modaloperators ausdrücken; in der natürlichen Sprache kann man dies analog durch die Stellung des Ausdrucks „notwendig“ (bzw. „möglich“) andeuten.

Als Beispiel stelle man sich vor, dass zwei Spieler gegeneinander eine Partie Backgammon spielen. Da es beim Backgammon kein Unentschieden gibt, gilt der folgende Satz:

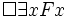$\Box \exists x Fx$ – Notwendig wird einer der Spieler gewinnen.

Dies bedeutet, egal wie das Spiel verläuft, einer der beiden Spieler wird am Ende der Sieger sein. Unter dieser Lesart, der de-dicto-Lesart, ist der Satz wahr. De re verstanden, lautet der Satz:

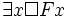$\exists x \Box Fx$ – Einer der Spieler wird notwendig gewinnen.

Man beachte, dass hier Existenzquantor (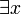$\exists x$) und Notwendigkeitsoperator ($\Box$) ihre Plätze getauscht haben. Der Satz bedeutet, dass es einen der beiden Spieler gibt, der in jedem Fall, egal wie das Spiel verläuft, gewinnt, und dies ist falsch, da beide Spieler die Chance haben, zu gewinnen.

Kritik an der „de re“-Notwendigkeit

Manche Philosophen lehnen die Annahme einer de-re-Modalität ab und halten nur die de-dicto-Modalität für sinnvoll. Nach dieser Auffassung liegt Notwendigkeit in der Sprache begründet und macht es keinen Sinn, Dingen als solchen notwendige Eigenschaften zuzuschreiben.

In diesem Sinne liest man etwa bei dem amerikanischen Philosophen Willard Van Orman Quine: „Insoweit wir rein bezeichnend von [einem] Gegenstand sprechen, [...] ist es nicht einmal andeutungsweise sinnvoll, einige seiner Eigenschaften als notwendig und andere als kontingent einzustufen.“ (Wort und Gegenstand, § 41). Ein Hintergrund dafür ist, dass es schwierig oder unmöglich ist, Kriterien für die Unterscheidung zwischen notwendigen und nicht-notwendigen Eigenschaften anzugeben; ein anderer sind paradoxe oder überraschende Konsequenzen: „Es ist denkbar, dass man sagt, Mathematiker seien notwendigerweise rational und nicht notwendigerweise zweibeinig, während Radfahrer notwendigerweise zweibeinig, aber nicht notwendigerweise rational seien. Wie verhält es sich nun mit einem Individuum, das sowohl Mathematik als auch Radfahren zu seinen Besonderheiten zählt? Ist dieses konkrete Individuum notwendig rational und kontingent zweibeinig oder umgekehrt?“ (Wort und Gegenstand, § 41, beide Zitate Seite 344f. in der Reclam-Ausgabe)

Ein Verteidiger der de-re-Notwendigkeit ist dagegen Saul Aaron Kripke. Er argumentiert dafür, dass die Vorstellung einer beschreibungsunabhängigen Notwendigkeit oder Möglichkeit von Eigenschaften intuitiven Gehalt habe: In seinem Beispiel sagt jemand, indem er auf Nixon zeigt: „Das ist der Mann, der hätte verlieren können.“ (Es geht um die US-Präsidentschaftswahl 1968.) Die hier Nixon zugeschriebenen Eigenschaft ist eine de-re-Möglichkeit, die Nixon unabhängig von einer Beschreibung zukommt, es wäre daher nach Kripke gänzlich unintuitiv zu antworten: „O nein, wenn Sie ihn als ‚Nixon‘ beschreiben, dann hätte er verlieren können; aber wenn man ihn als den Gewinner beschreibt, stimmt es natürlich nicht, dass er hätte verlieren können.“ (Name und Notwendigkeit 1.Vortrag, Seite 51 in der Suhrkamp-Ausgabe). Das Vorhandensein dieses intuitiven Gehalts ist für Kripke „eine sehr beweiskräftige Evidenz“ dafür, dass es wesentliche Eigenschaften und damit de-re-Modalitäten gibt (ebd. Seite 51).

Literatur

• Saul A. Kripke, Ursula Wolf (Übers.): Name und Notwendigkeit. Frankfurt am Main, Suhrkamp 1993, ISBN 3-518-28656-0
• Willard Van Orman Quine: Wort und Gegenstand. Stuttgart, Reclam 1980, ISBN 3-15-009987-0

Weblinks

• Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)Vorlage:SEP/Wartung/Parameter 1 und weder Parameter 2 noch Parameter 3