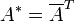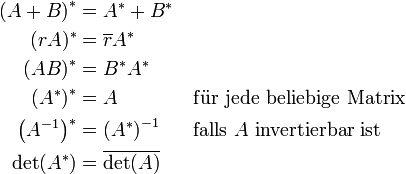- Adjungierte
-
In der linearen Algebra ist die zu einer reellen oder komplexen quadratischen Matrix A adjungierte Matrix A * eine Matrix, die eine bestimmte Vertauschungsbedingung für Skalarprodukte erfüllt.
Andere Schreibweisen für die adjungierte Matrix sind
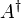 , AH und
, AH und 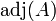 . Die Notation
. Die Notation 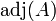 ist jedoch nicht eindeutig, da sie auch für die Adjunkte bzw. komplementäre Matrix verwendet wird.
ist jedoch nicht eindeutig, da sie auch für die Adjunkte bzw. komplementäre Matrix verwendet wird.Definition
Sei A eine
 -Matrix über dem Körper
-Matrix über dem Körper 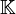 der reellen oder komplexen Zahlen, d.h.
der reellen oder komplexen Zahlen, d.h. 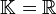 oder
oder 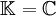 .
.Die zu A adjungierte Matrix A * ist durch folgende Eigenschaft definiert:
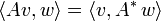 für alle
für alle 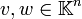 .
.
Dabei bezeichnet
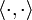 das kanonische Skalarprodukt des
das kanonische Skalarprodukt des 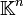 .
.Berechnung und Rechenregeln
Ist A eine reelle Matrix, dann ist die zu A adjungierte Matrix die Transponierte von A:
- A * = AT
Ist A eine komplexe Matrix, dann ist die zu A adjungierte Matrix die Transponierte der komplex Konjugierten von A:
Gilt A * = A, so heißt A selbstadjungiert. Im reellen Fall heißt die Matrix dann auch symmetrisch und im komplexen Fall auch hermitesch.
Im Folgenden seien A und B Matrizen und r eine komplexe Zahl, dann gilt:
Verallgemeinerung
In der Funktionalanalysis wird die adjungierte Matrix zum adjungierten Operator verallgemeinert.
Für einen Endomorphismus
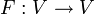 eines Hilbertraums V wird ein adjungierter Endomorphismus
eines Hilbertraums V wird ein adjungierter Endomorphismus 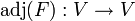 durch die Eigenschaft:
durch die Eigenschaft: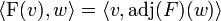 für alle
für alle 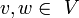
definiert. Man kann dann einen Zusammenhang zum dualen Operator
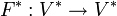 herstellen.
herstellen.
Wikimedia Foundation.