Differentialstruktur

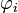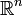
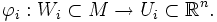
Eine differenzierbare Struktur (auch Differentialstruktur) beschreibt wichtige Eigenschaften einer Mannigfaltigkeit, die zwischen denen der Topologie und Geometrie liegen. Eine Mannigfaltigkeit wird dabei durch Karten $\varphi_{i}$ beschrieben, d.h. durch homöomorphe Abbildungen der Mannigfaltigkeit M in den linearen Raum $\mathbb{R}^{n}$

$\varphi_{i}:W_{i}\subset M\rightarrow U_{i}\subset\mathbb{R}^{n}.$

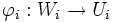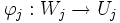Die Karten beschreiben mittels des linearen Raumes die lokalen Eigenschaften der Mannigfaltigkeit. Weitaus interessanter ist jedoch die Struktur zwischen den Karten: Gegeben seien zwei Karten $\varphi_{i}:W_{i}\rightarrow U_{i}$ und $\varphi_{j}:W_{j}\rightarrow U_{j}$. 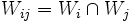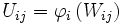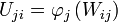Der Durchschnitt der Urbilder $W_{ij}=W_{i}\cap W_{j}$ wird in zwei (meist unterschiedliche) Bilder $U_{ij}=\varphi_{i}\left(W_{ij}\right)$ und $U_{ji}=\varphi_{j}\left(W_{ij}\right)$ abgebildet. Eine Koordinatentransformation zwischen den Karten ist eine Abbildung von Teilmengen des linearen Raumes:

$\varphi_{ij}:U_{ij}\rightarrow U_{ji},\,\,\varphi_{ij}(x)=\varphi_{j}\left(\varphi_{i}^{-1}\left(x\right)\right).$

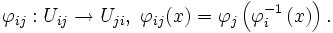
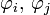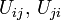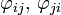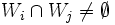Zwei Karten $\varphi_{i},\,\varphi_{j}$ sind kompatibel, wenn $U_{ij},\, U_{ji}$ offen (möglicherweise leer) sind, und die Koordinatentransformationen $\varphi_{ij},\,\varphi_{ji}$ (mit $W_{i}\cap W_{j}\neq\emptyset$) Diffeomorphismen sind. Eine Familie kompatibler Karten, die die ganze Mannigfaltigkeit überdeckt, wird Atlas genannt und zwei Atlanten sind äquivalent, wenn alle ihre Karten kompatibel sind. Die Äquivalenzklassen von Atlanten bezüglich dieser Äquivalenzrelation sind die differenzierbaren Strukturen der Mannigfaltigkeit.

Für Mannigfaltigkeiten der Dimension kleiner als vier gibt es (bis auf Diffeomorphismus) nur eine differenzierbare Struktur. Für alle Mannigfaltigkeiten der Dimension größer als vier existieren nur endlich viele differenzierbare Strukturen. Die folgende Tabelle enthält die Zahl der differenzierbaren Strukturen auf den Sphären bis zur Dimension 11:

1	2	3	4	5	6	7	8	9	10	11
1	1	1	$\infty$	1	1	28	2	8	6	992

Mannigfaltigkeiten der Dimension vier sind bezüglich der differenzierbaren Strukturen außergewöhnlich: Die meisten kompakten 4-Mannigfaltigkeiten besitzen eine abzählbar unendliche Zahl von differenzierbaren Strukturen und die meisten nichtkompakten 4-Mannigfaltigkeiten sogar überabzählbar viele.

Siehe auch

• Atlas
• Mannigfaltigkeit