- Dijkstras Algorithmus
-
Der Algorithmus von Dijkstra (nach seinem Erfinder Edsger W. Dijkstra) dient der Berechnung eines kürzesten Pfades zwischen einem Startknoten und einem beliebigen Knoten in einem kantengewichteten Graphen. Die Gewichte dürfen dabei nicht negativ sein. Für Graphen mit negativen Gewichten aber ohne negative Zyklen ist der Bellman-Ford-Algorithmus geeignet.
Für nicht zusammenhängende, ungerichtete Graphen kann der Abstand zu bestimmten Knoten auch unendlich sein, wenn ein Pfad zwischen Startknoten und diesen Knoten nicht existiert, dieser aber in der Knotenmenge selbst vorliegt. Dasselbe gilt auch für gerichtete, nicht stark zusammenhängende Graphen.
Inhaltsverzeichnis
Algorithmus
Informeller Algorithmus
Die Grundidee des Algorithmus ist, ab einem Startknoten die kürzest möglichen Wege weiter zu verfolgen und längere Wege beim Updaten auszuschließen. Er besteht im wesentlichen aus diesen Schritten:
- Initialisierung aller Knoten mit der Distanz "unendlich", die des Startknotens mit 0.
- Markierung der Distanz des Startknotens als permanent, alle anderen Distanzen als temporär.
- Setze Startknoten als aktiv.
- Berechne die temporären Distanzen aller Nachbarknoten des aktiven Knotens durch Addition von dessen Distanz mit den Kantengewichten.
- Wenn eine solche berechnete Distanz für einen Knoten kleiner ist als die aktuelle, aktualisiere die Distanz und setze den aktuellen Knoten als Vorgänger. Dieser Schritt wird auch als Update bezeichnet und ist die zentrale Idee von Dijkstra.
- Wähle einen Knoten mit minimaler temporärer Distanz als aktiv. Markiere seine Distanz als permanent.
- Wiederhole 4-7, bis es keinen Knoten mit permanenter Distanz gibt, dessen Nachbarn noch temporäre Distanzen haben.
Algorithmus in Pseudocode
G bezeichnet einen gewichteten Graphen mit V als Menge von Knoten, E als Menge von Kanten und w als Gewichtsfunktion, welche die Kanten auf positive reelle Zahlen abbildet.
Im Pseudocode steht A für den Graphen mit den Knoten, für die die Abstände minimal sind (also der resultierende Graph). X ist ein Teilgraph von G, in denen die Kanten nicht notwendig minimal sind. Es gilt:
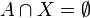 . d(v) bezeichnet die temporäre Distanz eines Knoten.
. d(v) bezeichnet die temporäre Distanz eines Knoten.foreach v in V(G) do d(v) =
 A := gb // A ist der auszugebende Graph
d(a) := 0
X :=
A := gb // A ist der auszugebende Graph
d(a) := 0
X := 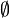 // X und d initialisieren
foreach z : z in
// X und d initialisieren
foreach z : z in 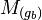 do
X := X
do
X := X  {z}
d(z) := w(gb,z)
while (X !=
{z}
d(z) := w(gb,z)
while (X !=  ) do
// wähle y als das Element von X mit dem kleinsten Wert von d(v)
y : (y in X) and (d(y) =
) do
// wähle y als das Element von X mit dem kleinsten Wert von d(v)
y : (y in X) and (d(y) = 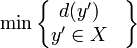 // füge A y hinzu und lösche es gleichzeitig aus X
A.add(y);
X.remove(y);
foreach z: z
// füge A y hinzu und lösche es gleichzeitig aus X
A.add(y);
X.remove(y);
foreach z: z 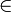 M_(y) and !(z
M_(y) and !(z 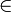 A) do
if !(z
A) do
if !(z 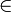 X) then
X := X
X) then
X := X 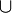 {z}
d(z) := d(y) + w(y,z)
else
/*
* somit ist z
{z}
d(z) := d(y) + w(y,z)
else
/*
* somit ist z 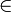 X
*/
d(z) :=
X
*/
d(z) := 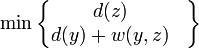
Beispiel
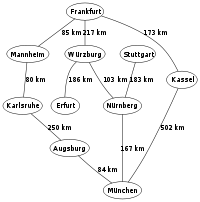
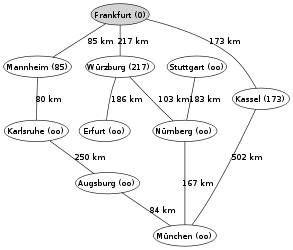
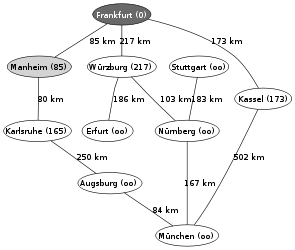
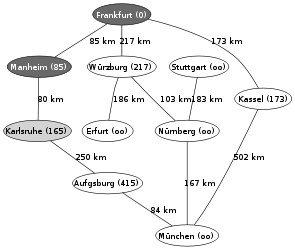
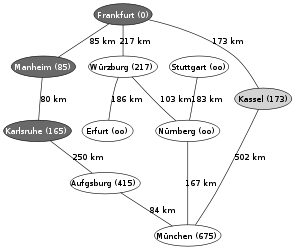
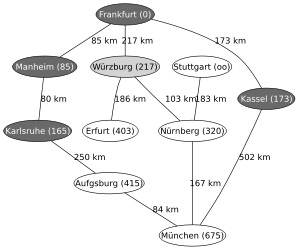
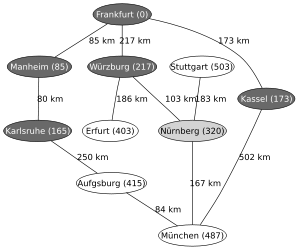
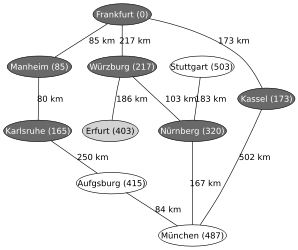
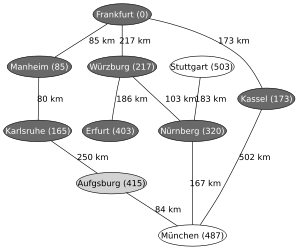
Ein Beispiel für die Anwendung des Algorithmus von Dijkstra ist die Suche nach einem kürzesten Pfad auf einer Landkarte. Im hier verwendeten Beispiel will man in der rechts gezeigten Landkarte von Deutschland einen kürzesten Pfad von Frankfurt nach München finden. Die Zahlen auf den Verbindungen zwischen zwei Städten geben jeweils die Entfernung zwischen den beiden durch die Kante verbundenen Städten an.
Beispiel Grundlegende Konzepte und Verwandtschaften
Ein alternativer Algorithmus zur Suche kürzester Pfade, der sich dagegen auf das Optimalitätsprinzip von Bellman stützt, ist der Floyd-Warshall-Algorithmus. Das Optimalitätsprinzip besagt, dass, wenn der kürzeste Pfad von A nach C über B führt, der Teilpfad A B auch der kürzeste Pfad von A nach B sein muss.
Ein weiterer alternativer Algorithmus ist der A*-Algorithmus, der den Algorithmus von Dijkstra um eine Abschätzfunktion erweitert. Falls diese gewisse Eigenschaften erfüllt, kann damit der kürzeste Pfad unter Umständen schneller gefunden werden.
Berechnung eines Spannbaumes
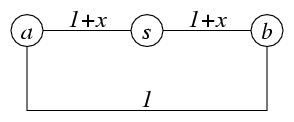
Nach Ende des Algorithmus ist in den Vorgängerzeigern π ein spannender Baum der Komponente von
 aus kürzesten Pfaden von
aus kürzesten Pfaden von  zu allen Knoten der Komponente verzeichnet. Dieser Baum ist jedoch nicht notwendigerweise auch minimal, wie die Abbildung zeigt:
zu allen Knoten der Komponente verzeichnet. Dieser Baum ist jedoch nicht notwendigerweise auch minimal, wie die Abbildung zeigt:Sei
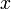 eine Zahl größer 0. Minimal spannende Bäume sind entweder durch die Kanten
eine Zahl größer 0. Minimal spannende Bäume sind entweder durch die Kanten 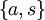 und
und 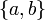 oder
oder 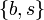 und
und 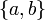 gegeben. Die Gesamtkosten eines minimal spannenden Baumes betragen
gegeben. Die Gesamtkosten eines minimal spannenden Baumes betragen 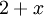 . Dijkstras Algorithmus liefert mit Startpunkt
. Dijkstras Algorithmus liefert mit Startpunkt  die Kanten
die Kanten 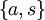 und
und 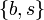 als Ergebnis. Die Gesamtkosten dieses spannenden Baumes betragen
als Ergebnis. Die Gesamtkosten dieses spannenden Baumes betragen 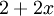 .
.Die Berechnung eines minimalen Spannbaumes ist mit dem Algorithmus von Prim oder dem Algorithmus von Kruskal möglich.
Zeitkomplexität
Im Folgenden sei m die Anzahl der Kanten und n die Anzahl der Knoten.
Die Zeitkomplexität des Algorithmus hängt in hohem Maße von der Datenstruktur ab, welche zur Speicherung der noch nicht besuchten Knoten (Q) benutzt wird. Im Normalfall wird man hier auf eine Vorrangwarteschlange zurückgreifen, indem man dort die Knoten als Elemente mit ihrer jeweiligen bisherigen Distanz als Schlüssel/Priorität verwendet.
Betrachtet man den Algorithmus unter diesem Aspekt ergibt sich folgender Aufwand:
Das „Füllen“ von Q in Zeile 02 wird dadurch erreicht, dass man jeden Knoten sowie seine Priorität (= Distanz) mittels insert in die Warteschlange einfügt; das wird, da es insgesamt n Knoten gibt, n Mal durchgeführt.
Da in Zeile 04 jeweils ein Knoten aus Q (bzw. der Warteschlange) entfernt wird, folgt, dass die Schleife in Zeile 03 ebenfalls n Mal durchlaufen wird (ein evtl. früherer Abbruch wegen Erreichen von g sei hier ausgenommen). In jedem Schleifendurchlauf muss geprüft werden, ob die Warteschlange leer ist (empty, Zeile 03) und es muss das nächste Element mit der niedrigsten Priorität entfernt werden (extractMin, Zeile 04); die beiden Operationen werden also jeweils n Mal durchgeführt.
Die Anzahl Aufrufe der relax Funktion kann zwar für jeden Durchlauf der Schleife in Zeile 07 variieren (da die Anzahl der von jedem Knoten u ausgehenden Kanten natürlich unterschiedlich sein kann), insgesamt über die Laufzeit des gesamten Algorithmus gesehen wird die Schleife aber m Mal ausgeführt, da jeder Knoten nur einmal betrachtet wird, und somit jede von ihm ausgehende Kante ebenfalls nur einmal betrachtet werden kann. Es werden somit alle ausgehenden Kanten aller Knoten im Graphen überprüft und damit erhält man natürlich alle Kanten des Graphen, also m Stück).
Sollte sich hier die bisher berechnete Distanz des Knotens v verringern, muss natürlich auch die Priorität in der Warteschlange mittels decreaseKey entsprechend verringert werden. Das passiert im Worst Case (im – unwahrscheinlichen – Fall dass die Überprüfung jeder Kante einen kürzeren Weg liefert) höchstens m Mal.
Der Vollständigkeit halber sollte man außerdem auch noch das Setzen von d[v] und π[v] in der relax Funktion betrachten, jedoch lässt sich dies jeweils in konstanter Zeit mit der Komplexität realisieren.
Insgesamt ergibt sich also eine Komplexität von
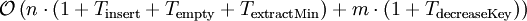 .
.Würde man zur Verwaltung der Knoten nun z. B. einfach eine Liste verwenden, ergäbe das eine Laufzeit von
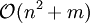 ; insert, empty und decreaseKey lassen sich alle in
; insert, empty und decreaseKey lassen sich alle in 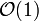 realisieren, das Suchen des Elements mit der kleinsten Priorität erfordert eine lineare Suche mit
realisieren, das Suchen des Elements mit der kleinsten Priorität erfordert eine lineare Suche mit 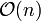 .
.Besser fährt man hier mit der Verwendung der Datenstruktur Fibonacci-Heap. Diese ermöglicht es ebenfalls, die Operationen insert, empty und decreaseKey (amortisiert betrachtet) in
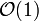 zu realisieren, die Komplexität von extractMin ist hier
zu realisieren, die Komplexität von extractMin ist hier 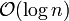 . Die gesamte Laufzeit beträgt dann lediglich
. Die gesamte Laufzeit beträgt dann lediglich 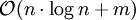 .
.Anwendungen
Routenplaner sind ein prominentes Beispiel, bei dem dieser Algorithmus eingesetzt werden kann. Der Graph repräsentiert hier das Straßennetz, welches verschiedene Punkte miteinander verbindet. Gesucht ist die kürzeste Route zwischen zwei Punkten.
Einige topologische Indizes, etwa der J-Index von Balaban, benötigen gewichtete Distanzen zwischen den Atomen eines Moleküls. Die Gewichtung ist in diesen Fällen die Bindungsordnung.
Der Dijkstras Algorithmus wird auch im Internet als Routing-Algorithmus im OSPF- und OLSR-Protokoll eingesetzt. Das letztere Optimized Link State Routing-Protokoll ist eine an die Anforderungen eines mobilen drahtlosen LANs angepasste Version des Link State Routing. Es ist wichtig für mobile Ad-hoc-Netze. Eine mögliche Anwendung davon sind die Freien Funknetze.
Andere Verfahren zur Berechnung kürzester Pfade
Weiß man genug über die einzelnen Kantengewichte des Graphen, um daraus eine Heuristik für die Kosten der einzelnen Knoten ableiten zu können, ist es möglich den Algorithmus von Dijkstra mittels dieser Heuristik zum A*-Algorithmus zu erweitern. Um alle kürzesten Pfade von einem Knoten zu allen anderen Knoten in einem Graphen zu berechnen, kann man den Bellman-Ford-Algorithmus verwenden, welcher auch mit negativen Kantengewichten umgehen kann. Der Algorithmus von Floyd und Warshall berechnet schlussendlich nicht nur die kürzesten Pfade eines Knotens zu allen anderen Knoten im Graph, sondern die kürzesten Pfade aller Knoten zueinander.
Literatur
- E. W. Dijkstra: A note on two problems in connexion with graphs. In: Numerische Mathematik. 1 (1959), S. 269–271
- Th. H. Cormen/C. E. Leiserson/R. Rivest/C. Stein: Algorithmen – Eine Einführung. Oldenbourg Verlag 2004. ISBN 3-486-27515-1
Algorithmen zum Auffinden minimaler Spannbäume
Weblinks
- Java-Applet zu Dijkstra und anderen
- Interaktive Visualisierung und Animation von Dijkstra's Algorithmus, geeignet für Leute ohne Vorkenntnisse von Algorithmen
- Implementierung in C (englisch)
- Erklärung anhand eines analogen Modells und Weitere Informationen
- Öffentliche Softwarebibliothek in Java mit diesem und anderen Algorithmen
- Java Implementierung - Simulation / Auswertung
Wikimedia Foundation.