- Dirichletbedingung
-
Funktionen, insbesondere periodische Funktionen, werden in der Mathematik oft in Fourierreihen entwickelt. Die Dirichlet-Bedingung (benannt nach Peter Gustav Lejeune Dirichlet) gibt an, wann die Fourierreihe punktweise gegen die entwickelte Funktion konvergiert.
Sei f eine im Intervall [ − T / 2,T / 2] definierte Funktion, die folgende Eigenschaften erfüllt:- Das Intervall [-T/2,T/2] lässt sich in endlich viele Teilintervalle zerlegen, in denen f(t) stetig und monoton ist.
- Ist t0 eine Unstetigkeitsstelle von f(t), so existieren rechts- und linksseitiger Grenzwert, f(t0 + ) und f(t0 − )
Dann konvergiert die Fourierreihe in jedem
![t \in [-T/2,T/2]](/pictures/dewiki/52/4ef82cc6f29dbfd4d268b4b633be72c0.png) gegen
gegen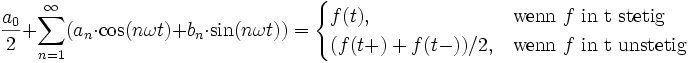 .
.
Wikimedia Foundation.
