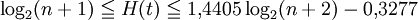Doppelrotation

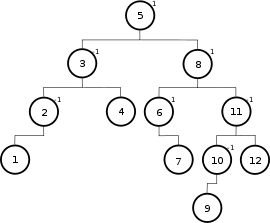
Ein AVL-Baum mit Balance-Angaben

Ein AVL-Baum ist eine Datenstruktur in der Informatik, genauer ein balancierter binärer Suchbaum. Als Invariante beim AVL-Baum gilt, dass sich für jeden Knoten k die Höhen h₁ und h₂ der beiden Teilbäume um höchstens 1 unterscheiden. Da diese Bedingung verhindert, dass der Baum aus der Balance gerät, nennt man ihn auch „ausgeglichen“. Die Höhe eines AVL-Baums mit n Knoten liegt in O(log n) und damit auch die maximale Anzahl der Schritte, um ein Element zu finden oder festzustellen, dass es nicht enthalten ist.

Der Name AVL leitet sich von den Erfindern Adelson-Velsky und Landis ab, die diese Datenstruktur 1962 entwickelten.^[1] Der AVL-Baum ist damit die älteste Datenstruktur für ausgeglichene Bäume. Eine Alternative mit schwächeren Bedingungen ist der Rot-Schwarz-Baum.

Balance

Ein Binärbaum heißt AVL-Baum, wenn sich für jeden seiner Teilbäume die Höhen des linken und rechten Astes höchstens um 1 unterscheiden. Die Höhe eines Baumes heißt, die maximale Anzahl Stufen bis zu einem externen (untersten) Knoten (definiere dazu die Höhe des leeren Baumes als 0). Die Berechnung der Balance eines Knotens erfolgt dann folgendermaßen:

$\operatorname{bal}(t) = H(t_r) - H(t_l)$

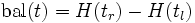
wobei t ein beliebiger Knoten im AVL-Baum ist und H(t_r) die Höhe des rechten Teilbaumes des Knotens t bezeichnet, H(t_l) analog die des linken Teilbaumes.

Ein binärer Suchbaum B ist genau dann ein AVL-Baum, wenn für alle Teilbäume c von B gilt: $\operatorname{bal}(c) \in \{ -1,0,1 \}$

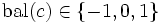
Die Höhe H(t) des AVL-Baums t mit n Knoten ist beschränkt durch:^[2]

$\log_2 (n + 1) \leqq H(t) \leqq 1{,}4405 \log_2 (n + 2) - 0{,}3277$

Zu einer gegebenen Höhe entspricht ein Fibonacci-Baum einem AVL-Baum mit minimaler Knotenanzahl, er ist also am schlechtesten ausgeglichen.

Operationen

Beim AVL-Baum gibt es drei Grundoperationen, das Suchen eines Elements, das den Baum unverändert lässt, sowie das Einfügen und das Löschen eines Elements. Wesentliche Eigenschaft des AVL-Baums ist, dass alle drei Operationen im schlechtesten Fall die Komplexität O(log n) haben.

Suchen eines Elements find

Die find-Operation ist im AVL-Baum die einfachste aller Operationen, und wird als grundlegende Operation sowohl in der insert-Operation als auch in der remove-Operation gebraucht. Der Suchbaum ist jederzeit so sortiert, dass rechts eines Knotens nur Knoten mit größeren Schlüsseln, und links vom Knoten nur Knoten mit kleineren (oder gleich großen) Schlüsseln gespeichert sind. Daher findet man einen Schlüssel, indem man von der Wurzel des Baumes schrittweise nach unten wandert, und dabei jeweils nach rechts verzweigt, falls der gesuchte Schlüssel größer als der des aktuellen Knotens ist, oder links wenn er kleiner(gleich) dem aktuellem Schlüssel ist. Stimmt der Schlüssel überein, hat man ihn gefunden; erreicht man ein Blatt, dessen Schlüssel nicht übereinstimmt, ist garantiert, dass der Schlüssel nicht im Baum existiert.

Einfügen eines Elements insert

Die insert-Operation versucht zuerst den Schlüssel mit der find-Operation zu finden. Scheitert dies, so ist das passende Blatt bekannt, das jetzt zum (inneren) Knoten wird. An diesem wird der neue Schlüssel als Blatt aufgehängt. Beim Rücksprung aus der rekursiven insert-Funktion wird geprüft, ob der Baum rebalanciert werden muss, und dies ggf. durchgeführt (s. u.). Der rekursive Rücksprung kann beendet werden, wenn die Balance eines Knotens zu 0, −1 oder 1 wird. Wird der Balance Faktor zu 0, hat sich die Tiefe des Teilbaumes nicht verändert, wird der Balancefaktor zu 2 bzw. −2, ist der Teilbaum des aktuellen Knotens unausgeglichen und muss rebalanciert werden (s. u.).

Entfernen eines Elements remove

Die remove-Operation sucht zuerst den Schlüssel wie die find-Operation und entfernt dann den entsprechenden Knoten. War es ein Blatt, geht es im Rücksprung des Rekursivaufrufs mit dem Rebalancieren weiter (s. u.), sonst müssen die beiden frei gewordenen Teilbäume neu aufgehängt werden. Dies wird realisiert, indem entweder der am weitesten links liegende Knoten des rechten Teilbaums oder der am weitesten rechts liegende Knoten des linken Teilbaums dazu benutzt wird, die beiden Teilbäume daran wieder aufzuhängen. Der Knoten nimmt den Platz des gelöschten Knotens ein und muss dabei natürlich selbst aus dem linken bzw. rechten Teilbaum des zu löschenden Knotens entfernt werden. Im nun folgenden Rücksprung werden die ggf. nötigen Rebalancierungen durchgeführt. Der rekursive Rücksprung kann beendet werden wenn der Balancefaktor eines Knotens zu 1 oder −1 wird. Wenn ein Balancefaktor zu 0 wird hat sich die Tiefe des Teilbaumes um 1 verringert und der rekursive Rücksprung muss weiter verfolgt werden. Wird ein Balancefaktor zu 2 oder −2 muss der Baum/Teilbaum rebalanciert werden (s.u).

Rebalancierung

Wurde durch eine Einfüge- bzw. Löschoperation die Balance zerstört, wird zusätzlich eine Rebalancierung durchgeführt. Dabei wird zwischen zwei Fällen unterschieden, der einfachen Rotation und der Doppelrotation.

Eine einfache Rotation ist immer dann notwendig, wenn sich durch das Einfügen oder Löschen eines Elements ein Höhenunterschied von mehr als 1 an einem der beiden äußersten Teilbäume eines Zweiges eines AVL-Baumes ergibt. Hingegen ist eine Doppelrotation notwendig, wenn der Höhenunterschied an inneren Teilbäumen auftritt.

Einfache Rotation

Abbildung 1: Einfache Rotation

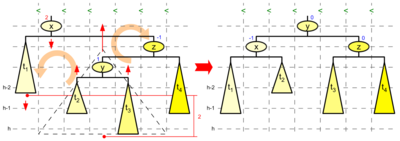
Die nebenstehende Abbildung zeigt eine einfache Rotation. Auf dem linken Bild ergibt sich nach einer Einfügung ein Höhenunterschied von zwei bei den beiden Teilbäumen von Knoten x. Da dieser Baum nicht mehr balanciert ist, muss eine Rebalancierung durchgeführt werden. Das Ergebnis dieser Operation ist auf der rechten Seite der Abbildung gezeigt.

Die Rebalancierung ändert lokal die Baumstruktur unter Beibehaltung der Sortierungsbedingung. Dazu werden einzelne Knoten und Teilbäume in der Hierarchie angehoben und andere abgesenkt. Dieses ist in der Abbildung durch senkrechte rote Pfeile dargestellt. Obwohl bei der Rebalancierung keine Seitwärtsverschiebung stattfindet, wird diese Operation als Rotation bezeichnet. Bei der gezeigten Rotation nach links (gegen den Uhrzeigersinn) wird Knoten y und Teilbaum t₃ um eine Ebene erhöht und Knoten x und Teilbaum t₁ um eine abgesenkt. Die Verknüpfungen werden entsprechend angepasst, so dass Teilbaum t₂ seinen Vaterknoten von y zu x wechselt und Knoten x und y ihre Position in der Hierarchie tauschen. Im resultierenden Baum ist die Balance wieder hergestellt. Zur dargestellten Rotation nach links, die den Teilbaum links außen absenkt und dafür den Teilbaum rechts außen erhöht, existiert eine spiegelbildliche Variante, die in einer Rotation nach rechts den linken Teilbaum erhöht und dafür den rechten absenkt.

Doppelrotation

Abbildung 2: Doppelrotation

Die in Abbildung 2 gezeigte Situation unterscheidet sich von der aus Abbildung 1 darin, dass die problematische Höhendifferenz zwischen dem linken Teilbaum t₁ und dem mittleren Teilbaum (mit Wurzel y) auftritt. Daher kann eine einfache Rotation wie in Abbildung 1, die den linken Teilbaum absenkt und dafür den rechten anhebt, keine Abhilfe schaffen. Es muss zunächst eine Rechtsrotation und anschließend eine Linksrotation durchgeführt werden. Diese Doppelrotation, deren Ergebnis auf der rechten Seite von Abbildung 2 gezeigt ist, hebt den mittleren Teilbaum um zwei Ebenen an und senkt dafür den linken um eine Ebene ab. Dazu wird der Wurzelknoten y des mittleren Teilbaumes um zwei Ebenen erhöht und wird damit neuer Vaterknoten von x und z. Die dadurch entstehenden freien Teilbäume t₂ und t₃ werden an die Knoten x und z aufgeteilt. Auch bei der sog. Doppelrotation geschehen keine Seitwärtsverschiebungen, wodurch die Sortierreihenfolge t₁ < x < t₂ < y < t₃ < z < t₄ der Knoten im AVL-Baum erhalten bleibt. Auch von der Doppelrotation existiert eine spiegelbildliche Variante, die ebenfalls den mittleren Teilbaum erhöht, dafür aber den rechten absenkt.

Nach einer Einfügung kann die Balance immer mit einer Rotationsoperation wiederhergestellt werden. Nach einer Löschoperation können mehrere Rebalancierungen vom jeweiligen Teilbaum aus bis hinauf zur Wurzel notwendig sein, um die Balance wiederherzustellen.

Implementierung

Jeder Knoten des Baums muss neben dem Schlüssel einen Balance-Wert speichern, der angibt ob der Baum links- oder rechtslastig ist. Der Balancegrad eines Knotens k berechnet sich aus („Höhe des rechten Teilbaums“) − („Höhe des linken Teilbaums“). Er beträgt 0, wenn der Knoten ausgeglichen ist (also linker und rechter Teilbaum gleich tief sind); er ist positiv, wenn der rechte Teilbaum tiefer als der Linke ist und negativ, wenn der Linke tiefer als der Rechte ist. Bei einem Balance-Wert größer 1 oder kleiner −1 ist eine Rotation erforderlich.

Nach jedem Einfügen oder Löschen eines Knotens wird in allen seinen Vorgängern bis zur Wurzel der Balance-Wert angepasst und die Balancierung überprüft. Dies geschieht auf dem „Rückweg“ der rekursiven Aufruffolge, was einen separaten Prüf- und Korrekturlauf überflüssig macht. Eine Rotation benötigt nur eine konstante Anzahl von Verknüpfungsänderungen am betreffenden Knoten, seinem Vorgänger und den beiden Nachfolgern.

Siehe auch

• B-Baum
• Rot-Schwarz-Baum

Literatur

• Ralf Hartmut Güting, Stefan Dieker: Datenstrukturen und Algorithmen. Stuttgart 2004, ISBN 9783519221210.
• Udi Manber: Introduction to Algorithms – A Creative Approach. 1989, Kapitel 4.3.4, S.75ff, Addison-Wesley Publishing Company.

Weblinks

• Algorithmenvisualisierung u.a. für AVL Bäume
• Ausführlichere Beschreibung mit Delphi-Programm
• Kurz gehaltene Beschreibung der Rotationen
• Java-Applet mit Animation (englisch)
• Animiertes Applet mit Sourcecode und ausführlicher Dokumentation
• Reich kommentierte iterative Implementierung von Herbert Glarner in Linoleum, einem plattformunabhängigen Assembler (englisch)
• Tutorial von Brad Appleton mit Implementierung in C++ (englisch)

Einzelnachweise

1. ↑ G. M. Adelson-Velsky, E. M. Landis: An algorithm for the organization of information (Englische Übersetzung aus Doklady Akademii Nauk SSSR 146). In: Soviet Math. Doklady. 3, 1962, S. 1259-1263
2. ↑ Donald E. Knuth: The Art of Computer Programming, Volume 3, Sorting and Searching, Second Edition. Addison-Wesley, 1998, ISBN 0-201-89685-0, 6.2.3 Balanced Trees, S. 458–478.