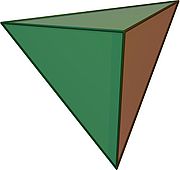
Pentatop

Regelmäßiger Pentachoron (5-Zeller)
Schlegeldiagramm (Ecken und Kanten)
Typ	Regelmäßiges Polychoron
Familie	Simplex
Zellen	5 (3.3.3)
Flächen	10 {3}
Kanten	10
Ecken	5
Eckfigur	(3.3.3)
Schläfli-Symbol	{3,3,3}
Coxeter-Dynkin-Diagramm
Symmetriegruppe	A4, [3,3,3]
Eigenschaften	konvex

Eckfigur: Tetraeder

Ein Pentachoron, (auch 5-Zeller, Pentatop oder Hyperpyramide genannt) ist ein 4-Simplex, das einfachste Polychoron (eine vierdimensionale Figur). Er besteht aus 5 teatraederförmigen Zellen und ist das Analog zum Dreieck (2-Simplex) und zum Tetraeder (3-Simplex).

Der regelmäßige Pentachoron ist einer der sechs regelmäßigen, konvexen Polychora und wird vom Schläfli-Symbol {3,3,3} repräsentiert.

Geometrie

Ein Pentachoron besteht aus fünf Zellen, die alle tetraederförmig sind. Seine Eckfigur ist ein Tetraeder. Seine maximale Durchschneidung mit dem dreidimensionalen Raum ist das Dreiecksprisma.

Bilder

Eine 3D-Projektion eines 5-Zellers, der eine Doppelrotation um zwei orthogonale Ebenen ausführt.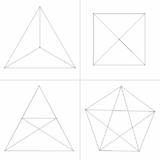

Vier orthographische Projektionen.

Konstruktion

Ein Pentachoron kann konstruiert werden, indem man zu einem Tetraeder eine fünfte Ecke hinzugefügt wird, die die gleiche Entfernung von den anderen Ecken hat wie die anderen Ecken untereinander. (Im Wesentlichen ist ein Pentachoron eine vierdimensionale Pyramide mit einer tetraederförmigen Basis.)

Projektionen

Eine mögliche Projektion des Pentachorons ist ein Pentagramm innerhalb eines Pentagons.

Beide, die Ecke-Zuerst- und die Zelle-Zuerst-Parallelprojektion des Pentachorons in drei Dimensionen, haben eine tetraederförmige Hülle. Das nächste bzw. die entfernteste Zelle wird auf den Tetraeder selbst projiziert, während die anderen vier Zellen auf die vier gestauchten tetraederförmigen Regionen, die das Zentrum umgeben, abgebildet werden.

Die Kante-Zuerst- und die Fläche-Zuerst-Projektion des Pentachorons in drei Dimensionen haben eine doppeldreieckspyramidenförmige Hülle. Zwei der Zellen werden auf die obere und untere Hälfte der Doppelpyramide während die übrigen drei auf drei nicht-regelmäßige tetraederförmige Körper um die zentrale Achse der Doppelpyramide mit Winkeln von jeweils 120° zueinander projiziert werden.

Alternative Namen

• 5-Zeller
• 4-Simplex
• Pentatop
• Hyperpyramide

Weblinks

• Platonische Polychora