- Drei-Dreiecke-Tangram
-
Das Drei-Dreiecke-Tangram (auch „Brügner’sche Dreiecke“) wurde von dem Mathematiker Georg Brügner († 1998) entwickelt [1]. Dabei handelt es sich um ein besonderes Tangram, das aus nur drei ähnlichen rechtwinkligen Dreiecken besteht, aus denen sich eine maximale Anzahl konvexer Figuren bilden lässt.
Im Gegensatz zu anderen Tangrams, deren Zweck ein eher spielerischer ist, basiert das Drei-Dreiecke-Tangram auf einem mathematischen Hintergrund.
Inhaltsverzeichnis
Aufbau des Tangrams
Aufbau des Tangrams
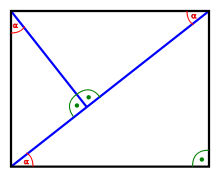
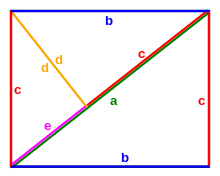
Wenn das Tangram wie im ersten Bild gebildet wird, entstehen drei rechtwinklige Dreiecke mit insgesamt sechs verschiedenen Seiten (die im zweiten Bild mit a bis f bezeichnet sind). Diese Dreiecke sind wegen der Gleichheit der Innenwinkel zueinander ähnlich.
Im Spezialfall f = c bestehen die Dreiecke nur aus fünf verschiedenen Seiten. Dieser Fall tritt genau dann ein, wenn die Diagonale a zur Seite c im Verhältnis Φ des Goldenen Schnittes steht, das heißt wenn
Seitenverhältnisse im Tangram
.
Für den zugehörigen Winkel α ergibt sich dann
Eine Besonderheit dieses Winkels ist außerdem die Beziehung cos 2α = sin α, aus der tan α = cos α folgt. Für die Seitenverhältnisse des Ausgangsrechteckes folgt dann
Nur bei diesem Seitenverhältnis im Ausgangsrechteck entsteht das Drei-Dreiecke-Tangram, da in diesem Fall die Anzahl konvexer Figuren maximal wird.
Die Figuren
Die 16 möglichen konvexen FigurenDadurch, dass die Dreiecke insgesamt nur fünf verschiedene Seiten haben, ergeben sich mehr Möglichkeiten, diese wieder zu Figuren zusammenzusetzen.
Es lassen sich genau folgende 16 verschiedene konvexe Figuren bilden:
- zwei Rechtecke,
- zwei gleichschenklige Dreiecke,
- zwei Parallelogramme,
- drei Trapeze,
- zwei Drachenvierecke,
- ein allgemeines Viereck,
- vier Fünfecke.
Einzelnachweise
Weblinks
Wikimedia Foundation.
