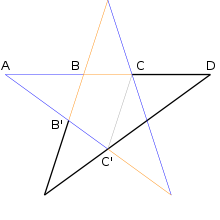Fünfeck

regelmäßiges Fünfeck

Ein Fünfeck (griechisch pentagon) ist eine geometrische Figur. Es gehört zur Gruppe der Vielecke (Polygone) und ist durch fünf Punkte definiert.

Mathematische Zusammenhänge

Sofern nichts anderes gesagt wird, ist von einem ebenen, regelmäßigen Fünfeck die Rede. Dieses besitzt fünf gleichlange Seiten und fünf gleichgroße Innenwinkel. Die fünf Eckpunkte liegen in einer Ebene.

Formeln

Größen eines regelmäßigen Fünfecks mit Kantenlänge a
Flächeninhalt	$A \, = \, \frac{a^2}{4} \sqrt{25 + 10\sqrt{5}}$
Umkreisradius	$r_u \, = \, \frac{a}{10} \sqrt{50 + 10\sqrt{5}}$
Inkreisradius	$r_i \, = \frac{a}{10} \sqrt{25 + 10\sqrt{5}}$
Diagonale	$d \, = \, \frac{a}{2} (1 + \sqrt{5})$
Höhe	$h \, = \frac{a}{2} \sqrt{5 + 2\sqrt{5}} = r_u + r_i$
Umfang	$u \, = 5 \, a$
Kantenwinkel = 108°	$\cos \, \alpha = \frac{1}{4}\left(1-\sqrt{5}\right)$

Beweis siehe Weblinks unten.

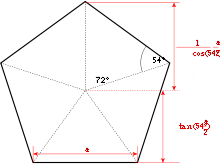
Formeln für Winkelberechnungen

Die Summe der Innenwinkel eines Fünfecks beträgt 540° und ergibt sich aus einer allgemeinen Formel für Polygone, in der für die Variable n die Anzahl der Eckpunkte des Polygons eingesetzt werden muss (in diesem Fall: n = 5):

$\sum {\alpha =}(n - 2) \cdot 180^\circ = 3 \cdot 180^\circ = 540^\circ$

Der Winkel, den zwei benachbarte Seitenkanten im ebenen, regelmäßigen Fünfeck miteinander einschließen, beträgt (wiederum nach einer allgemeinen Formel für regelmäßige Polygone)

$\alpha =\frac{(n - 2)}{n} \cdot 180^\circ = \frac{3}{5} \cdot 180^\circ = 108^\circ$

Reguläres Fünfeck

Formel für die Fläche A

Ein ebenes Fünfeck besitzt einen eindeutig bestimmbaren Flächeninhalt, welcher sich stets durch Zerlegen in Dreiecke berechnen lässt. Die Fläche eines regelmäßigen Fünfecks der Seitenlänge a ist das Fünffache der Fläche eines von seinem Mittelpunkt und zwei seiner Eckpunkte aufgespannten Dreiecks.

$A=5 \cdot \frac{1}{2} \cdot a \cdot \tan 54^\circ \cdot \frac{a}{2} = \frac{5}{4} \cdot a^2 \cdot \tan 54^\circ \approx a^2\cdot 1{,}7204774.$

Allgemein mit dem Umkreisradius r_u

$A=\frac{5}{8}\cdot r_u^2 \cdot \sqrt{10+2\sqrt 5}$

oder auch

$A=\frac{5}{2}\cdot r_u^2 \cdot \sin{72^\circ} \approx r_u^2 \cdot 2{,}3776413.$

Formel für die Seitenlänge a

$a=2 \cdot r_u \cdot \cos 54^\circ$

oder auch:

$a=r_u \cdot \sqrt{\frac{5 - \sqrt 5}{2}} \approx r_u \cdot 1{,}1755705$

zur Umrechnung siehe den Abschnitt über die als Quadratwurzeln angebbare Sinus- und Cosinus-Werte .

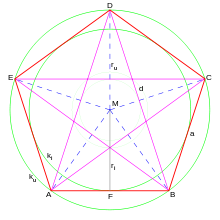
Der Goldene Schnitt im Fünfeck

Pentagramm

Regelmäßiges Fünfeck und Pentagramm bilden eine Grundfigur, in der das Verhältnis des Goldenen Schnittes wiederholt auftritt. Die Seite des Fünfecks befindet sich im goldenen Verhältnis zu seiner Diagonalen. Die Diagonalen untereinander teilen sich wiederum im goldenen Verhältnis, d. h. AD verhält sich zu BD wie BD zu CD. Der Beweis nutzt die Ähnlichkeit geeignet gewählter Dreiecke.

Konstruktion eines regelmäßigen Fünfecks mit Zirkel und Lineal

Konstruktion eines Fünfecks in einem umschließenden Kreis

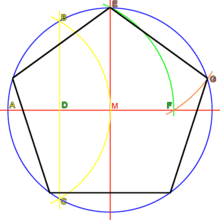
Für das regelmäßige Fünfeck existiert eine mathematisch exakte Konstruktion zur Bestimmung der Seitenlänge. Im Folgenden die Erläuterungen zur nebenstehenden Abbildung (Bild anklicken zeigt Vergrößerung; die Farben dienen zur besseren Veranschaulichung):

1. Zeichne einen Kreis (späterer Umkreis, blau) mit Radius r um den Mittelpunkt M.
2. Zeichne zwei zueinander senkrechte Durchmesser (rot) ein.
3. Halbiere einen Radius (gelb, Punkt D).
4. Zeichne einen Kreis (grün) mit dem Radius DE um Punkt D. Er schneidet die Gerade AM im Punkt F. Die Strecke EF ist die Länge der Seite.
5. Zum Abtragen auf dem Umkreis einen weiteren Kreisbogen (orange) mit Radius EF um E zeichnen. Er schneidet den ersten Kreis (blau) in G. Vorgang entsprechend wiederholen.

Berechnung zur Konstruktion:

$\overline{EM}= r \cdot 1$

$\overline{DM}= r \cdot \frac{1}{2}$

$\overline{DE}= r \cdot \sqrt{1+ \left(\frac{1}{2}\right)^2}$

$\overline{MF}= r \cdot \left(\sqrt{1+\left(\frac{1}{2}\right)^2}-\frac{1}{2} \right)$

$\overline{EF}= r \cdot \sqrt{1 + \left( \sqrt{1 + \left(\frac{1}{2}\right)^2}-\frac{1}{2} \right)^2}$

Umformen des Faktors:

$\frac{\overline{EF}}{r} = \sqrt{1+ \left( \sqrt{1 + \left(\frac{1}{2}\right)^2}-\frac{1}{2} \right)^2} = \sqrt{1 + \left( \sqrt{\frac{5}{4}} -\frac{1}{2} \right)^2}$

$\frac{\overline{EF}}{r} = \sqrt{1+ \left( \frac{\sqrt{5}}{2} -\frac{1}{2} \right)^2} = \sqrt{1 + \left( \frac{\sqrt{5}-1}{2} \right)^2}$

$\frac{\overline{EF}}{r} = \sqrt{1+ \frac{ 5- 2 \cdot \sqrt{5} + 1 }{4}} = \sqrt{ \frac{4}{4} + \frac{5-2 \cdot \sqrt{5} + 1 }{4}}$

$\frac{\overline{EF}}{r} = \sqrt{\frac{4+5- 2 \cdot \sqrt{5} +1}{4}} = \sqrt{\frac{10- 2 \cdot \sqrt{5}}{4}}$

$\frac{\overline{EF}}{r} = \sqrt{ \frac{5 - \sqrt{5}}{2}}$

Das entspricht genau dem Faktor in der obigen Formel für die Seitenlänge a.

Die Seitenkanten des Dreiecks MEF entsprechen exakt den Seitenlängen des regelmäßigen Sechsecks (ME), des regelmäßigen Fünfecks (EF) und des regelmäßigen Zehnecks (FM) mit dem gegebenen Umkreisradius r.

Mathematisch ausgedrückt:

1. Einen Kreis mit beliebigem Radius r mit dem Mittelpunkt M zeichnen und auf dem Durchmesser die Mittelsenkrechte konstruieren.
2. Die Schnittpunkte des Durchmessers mit dem Kreis werden mit A und X bezeichnet, die der Mittelsenkrechten mit E und Y. (X und Y fehlen in der Darstellung)
3. Zirkel in A einsetzen und AM=r auf dem Kreis abtragen. Die Schnittpunkte werden mit B und C bezeichnet. (gelber Kreis)
4. BC schneidet AM in D.
5. Zirkel in D einsetzen und DE auf AX abtragen, womit wir F erhalten.

ME ist die Seitenlänge des regelmäßigen Sechsecks, EF die des regelmäßigen Fünfecks und FM die des regelmäßigen Zehnecks mit dem gegebenen Umkreisradius r.

Bedeutung des Fünfecks in Architektur und Festungsbau

• 

  Zitadelle von Lille

• 

  Villa Farnese, Grundriss

• 

  Schloss Krzyżtopór

• 

  Pamplona im Jahr 1845

Der Grundriss einer neuzeitlichen bastionierten Festung hat häufig die Form eines Fünfecks. Anschauliche Beispiele für regelmäßige Fünfecke sind oder waren u.a. die vollständig wieder aufgebaute Festung Bourtange in den Niederlanden sowie die Zitadelle von Jaca, die Zitadelle von Pamplona, die Festung Dömitz, die Zitadelle von Turin, die Zitadelle von ’s-Hertogenbosch, die Zitadelle von Straßburg, die verschwundene Zitadelle von Antwerpen, die Zitadelle von Doullens (Picardie), die Zitadelle von Lille, das Harburger Schloss, die Zitadelle Vechta, Nieuw-Amsterdam (Suriname), das Kastell von Kopenhagen und die Höhenfestung Wülzburg bei Weißenburg in Bayern. Den Typ des befestigten Palasts (Palazzo in fortezza) auf regelmäßig fünfeckigem Grundriss verkörpern die Villa Farnese, die Schlösser Krzyżtopór und Nowy Wiśnicz sowie die Befestigungen von Schloss Łańcut in Polen.

Auch das Pentagon in Washington nutzt das regelmäßige Fünfeck als Grundriss. Es spielt damit jedoch nicht auf den alten Grundsatz der Konstruktion von Festungen an, sondern erhielt seine Form, weil es ursprünglich an einer anderen Stelle errichtet werden sollte, wo die Form durch die Grenzen des Grundstücks vorgegeben war.

Ein Fünfeck liegt auch der Anlage der Wallfahrtskirche Zelená Hora (Tschechische Republik) zugrunde.

Siehe auch: Fünfeckturm

Das Fünfeck in der zeitgenössischen Kunst

Pentagramm von Martina Schettina

Die Künstlerin Martina Schettina beschäftigt sich in ihren Werken mit den Eigenschaften von Fünfecken und dem darin auftretenden Goldenen Schnitt.^[1][2]

Das Fünfeck in der Natur

Okrafrüchte

Die Okra-Frucht hat im Querschnitt die Form eines Fünfecks. Die Blüten der Prunkwinde sind ebenfalls fünfeckig ausgebildet.

Bedeutung des Fünfecks im Motorenbau

Sternmotoren wurden meistens als 5, 7 oder 9-Zylinder gebaut.

Weblinks

 Commons: Fünfeck – Sammlung von Bildern, Videos und Audiodateien

 Wikibooks: Fünfeck – Lern- und Lehrmaterialien

Einzelnachweise

1. ↑ Martina Schettina:Mathemagische Bilder - Bilder und Texte. Vernissage Verlag Brod Media, Wien 2009, ISBN 978-3-200-01743-6.
2. ↑ Galerie in Virtuelles Freiberger Museum für Mathematik und Kunst