EPR-Paradox

Der EPR-Effekt (nach den Autoren des Artikels, in dem er das erste Mal behandelt wurde – Einstein, Podolski, Rosen -, zuweilen auch EPR-Paradoxon genannt), ist ein zunächst als Gedankenexperiment, später aber auch im Labor nachgewiesener Effekt in der Quantenmechanik, der explizit erkennen lässt, dass die Quantenmechanik gegen eine Grundannahme klassischer Theorien, den sog. lokalen Realismus, verstößt. In der ursprünglichen Formulierung ihres Gedankenexperiments ging es EPR darum nachzuweisen, dass die quantenmechanische Beschreibung der physikalischen Wirklichkeit, die in diesem Effekt „auf den Punkt gebracht“ wird, unvollständig sein müsse. Noch einfacher gesagt: Es wird gezeigt, dass die Quantenmechanik keine klassische Theorie ist.

Es gibt mehrere experimentelle Anordnungen, die das für das EPR-Experiment charakteristische Verhalten zeigen. Grundsätzlich weist ein solches EPR-artiges Experiment bzw. Gedankenexperiment stets folgende Charakteristika auf:

• Es wird ein System aus zwei Teilchen betrachtet, die anfänglich direkt miteinander wechselwirken und sich darauf weit voneinander entfernen (sog. „diametral auseinanderlaufende Teilchen“). Ein solches System wird durch einen einzigen, speziellen quantenmechanischen Zustand beschrieben, der kein Produktzustand ist, das heißt die beiden Teilchen befinden sich in einem speziellen verschränkten Zustand.
  • An den räumlich getrennten Teilchen werden zwei sog. komplementäre Messgrößen betrachtet, z. B. Ort und Impuls, oder zwei verschieden-gerichtete Drehimpulskomponenten. (Die gleichzeitige exakte Bestimmung dieser Messgrößen ist nach Heisenbergs Unbestimmtheitsrelation unmöglich.)
  • Es wird gezeigt, dass die Werte dieser Messgrößen für die beiden Teilchen, trotz der Trennung und trotz der Unschärferelation, streng korreliert sind: Eines der beiden Teilchen befindet sich nach der Messung in einem Eigenwert der ersten Messgröße, das andere im dazu komplementären Wert der zweiten Größe. (Welches der beiden Teilchen den Messwert "1" und welches "2" ergibt, das muss dabei nach den Gesetzen der Wahrscheinlichkeitsrechnung „erwürfelt“ werden.)

Am häufigsten wird heute die von David Bohm überarbeitete Fassung des EPR-Experiments diskutiert, in der zwei Teilchen mit Spin (Eigendrehimpuls) betrachtet werden, deren Gesamtspin (Summe der Spins der einzelnen Teilchen) Null ist. In dieser Neuformulierung ist das Experiment auch praktisch durchführbar. Einstein, Podolski und Rosen wählten ursprünglich Ort und Impuls der Teilchen als komplementäre Observable. Im Folgenden wird unten die bohmsche Variante vorgestellt. In den nächsten Abschnitten wird zunächst das Resultat des EPR-Experiments zusammengefasst und seine Bedeutung für die Interpretation der Quantenmechanik beschrieben. Anschließend werden die quantenmechanische Erklärung des Experiments und die zu ihrem Verständnis notwendigen Eigenschaften der Quantenmechanik kurz dargestellt.

Das EPR-Gedankenexperiment und seine Interpretation

Das ursprüngliche Argument von EPR für die Unvollständigkeit der Quantenmechanik

EPR betrachten als komplementäre Observable Ort und Impuls der beiden Teilchen. Es wird der Impuls von Teilchen 1 (T1) gemessen. Damit ändert sich der betrachtete verschränkte Zustand so, dass nun der Ausgang einer Impulsmessung an Teilchen 2 (T2) mit Wahrscheinlichkeit 1 exakt vorhergesagt werden kann. Dabei wurde Teilchen 2 sicher nicht durch eine unkontrollierte Wechselwirkung gestört. Es könnte stattdessen ebenso gut der Ort von Teilchen 1 bestimmt werden, wodurch, wieder ohne eine Störung, nun der Ort von Teilchen 2 exakt vorhersagbar wäre. Zum Schluss, dass die Quantenmechanik unvollständig ist, führen nun die folgenden Annahmen:

• In einer vollständigen Theorie muss jedes Element der physikalischen Realität eine Entsprechung haben.
• Eine physikalische Größe, deren Wert mit Sicherheit vorhersagbar ist, ohne das System, an dem sie gemessen wird, zu stören, ist ein Element der physikalischen Realität.

Da nun die Entscheidung, ob der Ort von Teilchen T2 oder sein Impuls durch Messung der jeweiligen Gegenstücke an Teilchen T1 bestimmt wird, erst kurz vor der Messung getroffen zu werden braucht, kann sie sicherlich keinen störenden Einfluss auf Elemente der Realität von T2 haben. Daraus schließen EPR, dass beide Größen Teil derselben physikalischen Realität sein müssten. Da aber nach der Quantenmechanik für jedes einzelne Teilchen nur jeweils eine der Größen vorhersagbar ist, ist die Quantenmechanik unvollständig.

Niels Bohr wandte gegen dieses Argument ein, dass der Begriff der störungsfreien Messung nicht angemessen definiert sei, wenn er sich auf eine mechanische Wechselwirkung in der letzten Phase des Experiments beschränke. Eine solche liege in der Tat nicht vor, dennoch schließe der Versuchsaufbau, der zur genauen Vorhersage des Ortes von T2 führe, eben das komplementäre Experiment zur Bestimmung seines Impulses aus, weshalb beide Größen nicht Elemente derselben Realität sondern Elemente zweier komplementärer Realitäten seien.

Das EPR-Experiment als Paradoxon

Gelegentlich ist auch vom EPR-Experiment als einem Paradoxon die Rede. Hierbei erscheint es auf den ersten Blick paradox, dass zwei komplementäre Observable eines Teilchens gleichzeitig bestimmt werden können (die eine etwa direkt durch Messung am ersten Teilchen, die andere indirekt durch Messung am zweiten Teilchen). Das ist scheinbar ein Widerspruch zu der bekannten Heisenbergschen Unschärferelation. In der Kopenhagener Deutung wird das Paradoxon aufgelöst mit dem Hinweis darauf, dass die indirekte Bestimmung über die Messung am zweiten Teilchen eben gar keine Messung der Eigenschaft des ersten Teilchens ist.

John Stewart Bell veranschaulichte die Fehler bei der Interpretation von Verschränkung und EPR-Effekt anhand des Vergleichs mit Bertlmanns Socken.

Lokale verborgene Variable und EPR-Korrelationsexperimente

Seit der EPR-Arbeit (1935) bis zu seinem Lebensende (1955) verfolgte Einstein, in der Erkenntnis, dass die Quantenmechanik, für sich allein genommen, dem „gesunden Menschenverstand“ widerspricht (- „Gott würfelt nicht“ - ), hartnäckig ein naheliegendes Ziel, das sich erst nachträglich, 1964, als von vornherein unmöglich erwies, weil sich die angenommenen Grundvoraussetzungen als falsch herausstellten, s.u.: Dieses Ziel war, die Quantenmechanik im Sinne von EPR zu vervollständigen.

Das sollte durch Einführung von verborgenen lokalen Variablen geschehen, die die Rolle der fehlenden „Elemente der Realität“ zu übernehmen hatten. Einsteins Grundannahmen implizieren aber die sog. Bellsche Ungleichung (Bell 1964), wobei sich ergibt, dass letztere mit der Quantenmechanik unverträglich ist; die Quantenmechanik verletzt diese Ungleichung, was definitiv zeigt, dass sie Aussagen macht, die – im Widerspruch zu Einstein – über die Grundannahmen klassischer Theorien hinausgehen.

Dadurch ergab sich die Möglichkeit, in konkreten Experimenten zwischen der Quantenmechanik oder den Einsteinschen Annahmen zu entscheiden.^[1]

Entsprechende Resultate (u. a. durch Alain Aspect) bestätigen die quantenmechanischen Vorhersagen und widerlegen den Einsteinschen lokalen Realismus. Sie zeigen eine (quantenmechanisch zulässige) Korrelation, die deutlich größer ist, als dies in einer klassischen Theorie, d.h. entsprechend der Bellschen Ungleichung, denkbar wäre.

Nach der sog. Kopenhagener Interpretation der Quantenmechanik (bei den Physikern seit Jahrzehnten „Standard“!) lässt sich dies durch folgende zwei "Statements" deuten:

1. Eine quantenmechanische Messung stellt nicht einfach den A-priori-Zustand eines Systems fest, sondern der quantenmechanische Zustand wird durch die Messung erst präpariert. Dadurch drückt sich die Nicht-Realität der Quantenmechanik aus.
2. Die Nicht-Lokalität ergibt sich letztlich aus der Tatsache, dass zu jedem Zeitpunkt durch einen einzigen abstrakten Zustandsvektor 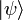$|\psi\rangle$ der Zustand des Systems gleichzeitig an allen Stellen (x,y,z) festgelegt ist, $|\psi\rangle \mapsto \psi (x,y,z)$.

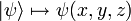Eine erste praktische Anwendung ist die Quantenkryptographie.

In diesem Zusammenhang verdient auch der sog. Aharonov-Bohm-Effekt Beachtung.

Es ist jedoch nicht möglich, mit Hilfe des EPR-Effekts mit Überlichtgeschwindigkeit zu kommunizieren: Die einzelne Messung ergibt – unabhängig davon, ob das andere Teilchen bereits gemessen wurde – stets ein für sich genommen unvorhersagbares Ergebnis. Erst, wenn das Ergebnis der anderen Messung – durch klassische, unterlichtschnelle Kommunikation – bekannt ist, kann man die Korrelation feststellen oder ausnutzen.

Quantentheoretische Grundlagen des EPR-Experiments

Spinorraum

Die Quantenmechanik des Spin-1/2-Freiheitsgrades eines Teilchens spielt sich in einem besonders einfachen Hilbertraum ab, dem 2-dimensionalen Spinorraum für ein einzelnes Teilchen. Darüber hinaus spielen nur ganz einfache Eigenschaften dieses Raumes für das EPR-Experiment eine Rolle.

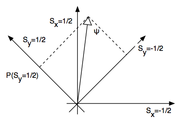
• Die erste ist die, dass die Eigenvektoren zweier nicht kommutierender Operatoren zwei verschiedene Basen desselben Unterraumes bilden. Das können wir uns an dem je einem der beiden Teilchen entsprechenden 2-dimensionalen Spinorraums wie in nebenstehender Abbildung veranschaulichen.
  

  Veranschaulichung des 2-dimensionalen Spinorraumes
  Die Abbildung zeigt als komplementäre Observable x- und y-Komponente des Spins in Form von um 45 Grad gegeneinander gedrehten Koordinatensystemen (die jeweils den Eigenvektorbasen der zu den Observablen gehörigen Operatoren entsprechen). Fällt man das Lot vom Zustandsvektor ψ auf die zu einem Messwert gehörige Koordinatenachse (den Eigenvektor zum Eigenwert), so erhält man die quantentheoretische Wahrscheinlichkeit dafür, bei einer Messung ebendiesen Messwert zu finden. Die Tatsache, dass diese Wahrscheinlichkeit offensichtlich nur für genau einen Wert einer der Observablen gleich eins sein kann, erklärt genau die Heisenbergsche Unbestimmtheitsrelation.
• Die zweite ist die Tatsache, dass der quantenmechanische Zustandsraum eines Mehrteilchensystems sich als das direkte Produkt der Zustandsräume seiner Bestandteile ergibt, man also als Zustandsvektor eines 2-Teilchen-Spin-1/2-Systems einen 4-dimensionalen, linearen Vektorraum erhält, der aus allen geordneten Paaren von Basisvektoren der 2-dimensionalen Spinorräume besteht. Das führt dazu, dass der Kollaps der Wellenfunktion durch Messung an einem Teilchen im Allgemeinen auch den Zustand des anderen Teilchens ändert (siehe nächsten Abschnitt).

Kollaps der Wellenfunktion

Der sog. Kollaps der Wellenfunktion müsste in unserem Bild besser Projektion des Zustandsvektors heißen. Sie wird in der Quantenmechanik postuliert, um die Präparation eines Systems bzw. den quantenmechanischen Messvorgang zu beschreiben. In den üblichen Deutungen der Quantenmechanik (Kopenhagener Interpretation und verwandte) wird die Projektion des Zustandsvektors als unabhängiges Postulat eingeführt: Wird an einem System eine Observable gemessen, geht sein Zustandsvektor sprunghaft in die Projektion des bisherigen Zustandsvektors auf den Eigenvektor zum gemessenen Eigenwert über. Bei einem verschränkten Zustand heißt das, dass sich damit der Zustand auch hinsichtlich der Wahrscheinlichkeiten für Messergebnisse am jeweils anderen System ändert. Sei etwa der Ausgangszustand (bis auf Normierung) 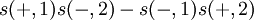$\,s(+,1) s(-,2) - s(-,1) s(+,2)$, wobei 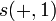$\,s(+,1)$ der Eigenvektor zur Messung eines positiven Spins in einer bestimmten Richtung ("x-Richtung") an System 1 sei. Durch Messung z. B. eines negativen Spins in x-Richtung an System 1 verschwinden nun alle Komponenten des Ausgangszustands, die den Eigenvektor zu positivem Spin bei Teilchen 1 enthalten. Der Zustand geht also über in 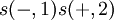$\,s(-,1) s(+,2)$, d.h. an Teilchen 2 wird eine weitere Messung des Spins in x-Richtung mit Sicherheit positiven Spin ergeben. Schreibt man die kollabierte Wellenfunktion in der Eigenvektorbasis der komplementären Observablen (Spin in y- oder x-Richtung, das gedrehte Koordinatensystem im Bild) hin, so sieht man, dass beide Werte in einer dieser Richtungen wieder gleich wahrscheinlich sind. Könnte also ein Beobachter von Teilchen 2 exakte Kopien von dessen Quantenzustand anfertigen, könnte er tatsächlich feststellen, welche Observable der Beobachter des ersten Teilchens gemessen hat, und es wäre ein (überlichtschneller) Informationsfluss von Beobachter 1 zu Beobachter 2 möglich. Derartige "Quantenverstärker" gibt es jedoch nicht.

Siehe auch

• GHZ-Zustand
• Quantenteleportation
• Quantenverschränkung
• Quantenmechanische Messung

Einzelnachweise

1. ↑ Bemerkung: Hier sieht man besonders deutlich, dass in der Physik letztlich das Experiment zählt.

Literatur

• A. Einstein, B. Podolsky, N. Rosen: Can quantum-mechanical description of physical reality be considered complete?, Phys. Rev. 47 (1935), S. 777 - 780 doi:10.1103/PhysRev.47.777
• D. Bohm, Y. Aharonov: Discussion of Experimental Proof for the Paradox of Einstein, Rosen and Podolsky, Phys. Rev. 108 (1957), S. 1070 - 1076 doi:10.1103/PhysRev.108.1070
• Alexander Afriat, Franco Selleri: The Einstein, Podolsky, and Rosen paradox in atomic, nuclear, and particle physics. Plenum Press, New York 1999, ISBN 0-306-45893-4

Weblinks

• Arthur Fine: „The Einstein-Podolsky-Rosen Argument in Quantum Theory“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
• László E. Szabó: „The Einstein-Podolsky-Rosen Argument and the Bell Inequalities“ in der Internet Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
• Franz Embacher: EPR-Paradoxon und Bellsche Ungleichung, Ms. Wien 2000
• Realexperiment zur Verschränkung: www.QuantumLab.de