Ekman-Tiefe

Darstellung der Ekman-Spirale (Nordhalbkugel, vereinfacht). 1:Wind 2:durch den Wind bestimmte Strömungsrichtung 3:Tatsächliche Strömungsrichtung 4: Coriolis-Effekt

Die Korkenzieherströmung, auch Ekman-Spirale (nach Vagn Walfrid Ekman), tritt überall da auf, wo Wind stetig über eine Wasserfläche weht.

Beschreibung

Bildlich gesehen zieht der Wind das Wasser durch Reibung hinter sich her. Sobald das Wasser sich in Bewegung setzt, lenkt es die Coriolis-Kraft auf der Nordhalbkugel nach rechts ab. Jede folgende Wasserschicht unter der Oberfläche wird durch die Reibung an der Oberfläche mitbewegt, und der Coriolis-Effekt dreht die Richtung des Geschwindigkeitsvektors dabei immer weiter nach rechts. Die Oberflächenströmung ist um 45° zur Windrichtung gedreht und erreicht nur etwa drei Prozent der Windgeschwindigkeit. Tiefere Wasserschichten bewegen sich immer langsamer und die Bewegungsrichtung weicht immer stärker von der Windrichtung ab. Schließlich fließt das Wasser in der so genannten Ekman-Tiefe sogar entgegengesetzt zur Windrichtung. Die Geschwindigkeit des Tiefenwassers ist hier auf ca. 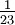$\tfrac{1}{23}$ der Oberflächengeschwindigkeit gesunken. Es handelt sich daher bei der Korkenzieherströmung um ein vertikales Geschwindigkeitsprofil (Gradient). Die Ekman-Tiefe wird auch als Grenze des Einflusses der Windreibung betrachtet. In mittleren Breiten liegt sie etwa bei 50 Meter.

Der gesamte Wassertransport von der Wasseroberfläche bis zur zweifachen Ekman-Tiefe geschieht dabei, auf der Nordhemisphäre, im rechten Winkel nach rechts. Zum Verständnis der windgetriebenen Zirkulation ist dies ein unverzichtbares Hilfsmittel.

Links: Kräfte auf ein Wasserteilchen im Kräftegleichgewicht: Die resultierende Strömung der Oberflächenschicht ist die Summe aus Windstress und Coriolis-Kraft, sie wird durch Reibung balanciert. Die Oberflächenströmung im idealisierten Modell weist auf der Nordhalbkugel vom Wind um 45° nach rechts ab.
Rechts oben: Dreidimensionale Veranschaulichung der Ekman-Spirale. Die Strömungsgeschwindigkeit nimmt exponentiell mit der Tiefe ab und dreht auf der Nordhalbkugel mit der Tiefe nach rechts.
Rechts unten: Draufsicht auf die Ekmanspirale. Das Integral über die Strömungen ergibt einen Nettotransport, der auf der Nordhalbkugel um 90° nach rechts vom Wind abweicht.

Genau wie es an der Wasseroberfläche eine Ekman-Spirale gibt, existiert auch eine Ekman-Spirale in der Luft über der Wasseroberfläche bzw. über dem Erdboden oder im Wasser über dem Meeresgrund, falls dieses Wasser strömt. Diese hat einen umgekehrten Drehsinn. Die resultierende Geschwindigkeit dreht also mit größerer Tiefe nach links (in der Nordhemisphäre). In flachem Wasser überlagern sich beide Spiralen. Ist das Wasser flach genug, weist die resultierende Wasseroberflächenströmung in Richtung des Windes.

Siehe auch

• Ekman-Transport, Geostrophie, Sverdrup-Transport
• Wasserwelle