Elliptische Koordinaten

Im elliptischen Koordinatensystem wird ein Punkt durch Angabe der Lage auf konfokalen Ellipsen und Hyperbeln bestimmt.

Bei zweidimensionalen elliptischen Koordinaten lautet die Umrechnung in kartesische Koordinaten

$\vec r=\begin{pmatrix} x \\ y \end{pmatrix} = C \cdot \begin{pmatrix} \cosh u \cdot \cos v \\ \sinh u \cdot \sin v \end{pmatrix}$

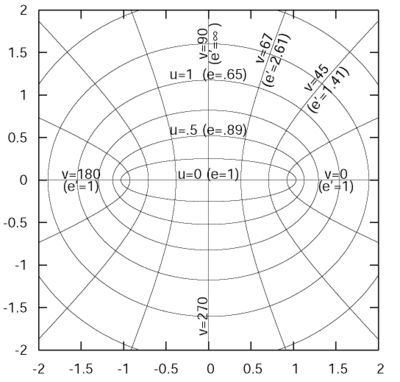
u und v sind hier die Koordinaten. C ist ein frei wählbarer Parameter aus der Menge der reellen Zahlen R. v läuft von 0 bis 2π. u ist nicht beschränkt. Allerdings ist für $u \in \left [0, \infty \right [$ bereits eine eineindeutige, d.h. bijektive Abbildung in die xy-Ebene gegeben. Die u-Koordinatenlinien sind Hyperbeln, die v-Koordinatenlinien Ellipsen. Für u=0 ist die v-Koordinatenlinie zu einer Strecke von $\begin{pmatrix} -C \\ 0 \end{pmatrix}$ bis $\begin{pmatrix} C \\ 0 \end{pmatrix}$ entartet. Für v=0 ist die u-Koordinatenlinie zu einer Halbgeraden entartet mit dem Wertebereich $\left [C, \infty \right [$. Für v=π ist die u-Koordinatenlinie die an der y-Achse gespiegelte Halbgerade entlang der negativen x-Achse. Für v=π/2 und v=3π/2 ist die u-Koordinatenlinie die y-Achse, bzw. die an der x-Achse gespiegelte y-Achse.

Alle Ellipsen und Hyperbeln haben die gleiche lineare Exzentrizität ae=C, wobei a die große Halbachse der Ellipse bzw. Hyperbel ist. Die numerische Exzentrizität einer Ellipse, auf der u=const ist, ist e=1/coshu. Die numerische Exzentrizität einer Hyperbel, auf der v=const ist, ist e=1/cosv.

Diese elliptischen Koordinaten können auf verschiedenen Arten auf den dreidimensionalen Raum erweitert werden. Bei zylindrischen elliptischen Koordinaten wird einfach die kartesische z - Koordinate als weitere Koordinate hinzugefügt. Bei polaren elliptischen Koordinaten wird die Ebene um einen Winkel θ gedreht, der dann die zusätzliche Koordinate bildet:

$\vec r=\begin{pmatrix} x \\ y \\ z \end{pmatrix} = C \cdot \left[\cosh u \cdot \cos v \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} + \sinh u \cdot \sin v \cdot \begin{pmatrix} 0 \\ \cos\theta \\ \sin\theta \end{pmatrix}\right]$

Schließlich gibt es noch räumlich elliptische Koordinaten:

$\vec r=\begin{pmatrix} x \\ y \\ z \end{pmatrix} = C \cdot \left[\cosh u \cdot \cos v \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} + \sinh u \cdot \sin v \cdot \begin{pmatrix} 0 \\ \cos\theta \\ b \cdot \sin\theta \end{pmatrix}\right]$

Hier ist b ein weiterer Parameter des Koordinatensystems. Die θ-Koordinatenlinien sind hier Ellipsen. v läuft hier von 0 bis π, u von 0 bis unendlich und θ von 0 bis 2π.

Anwendungen

Durch die Transformation auf elliptische Koordinaten kann die Schrödinger-Gleichung für das H₂⁺ - Molekül in Born-Oppenheimer-Näherung analytisch gelöst werden.