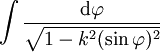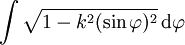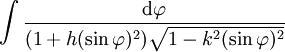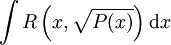elliptische Integrale — ellịptische Integrale, Integrale vom Typ wobei R eine rationale Funktion in zwei Variablen und P (x) ein Polynom dritten oder vierten Grades in x ohne mehrfache Nullstelle ist. Ein elliptisches Integral ist im Allgemeinen nicht durch… … Universal-Lexikon
Elliptische Integrale und Funktionen — Elliptische Integrale und Funktionen. Kommt in einem Integral unter dem Integralzeichen eine Quadratwurzel aus einem Ausdruck 3. oder 4. Grades in x vor, so wird dasselbe als ein elliptisches Integral bezeichnet. Man unterscheidet hierbei drei… … Lexikon der gesamten Technik
Elliptische Integral-Funktion — Ein Elliptisches Integral ist ein Integral vom Typ wobei R eine rationale Funktion in zwei Variablen und P(x) ein Polynom dritten oder vierten Grades ohne mehrfache Nullstelle ist. Der Name rührt daher, dass Integrale dieser Form bei der… … Deutsch Wikipedia
Elliptische Kurve — In der Mathematik ist eine elliptische Kurve eine singularitätenfreie algebraische Kurve der Ordnung 3 in der projektiven Ebene. Beispiel einer elliptischen Kurve über dem Körper der reellen Zahlen Elliptische Kurven über dem Körper der reellen… … Deutsch Wikipedia
Elliptische Functionen — (Elliptische Transscendenten), Functionen, deren Integrale von der Länge elliptischer Bogen abhängen, die bei gegebenen Halbachsen einer gewissen Abscisse entsprechen. Sie sind alle begriffen in dem Integrale: worin R eine rationale Function von… … Pierer's Universal-Lexikon
Elliptische Funktion — Im mathematischen Teilgebiet der Funktionentheorie sind elliptische Funktionen doppeltperiodische meromorphe Funktionen. „Doppeltperiodisch“ bedeutet, dass es zwei komplexe Zahlen ω1,ω2 gibt, die linear unabhängig im reellen Vektorraum sind, so… … Deutsch Wikipedia
Elliptische Funktionen — Im mathematischen Teilgebiet der Funktionentheorie sind elliptische Funktionen doppeltperiodische meromorphe Funktionen. „Doppeltperiodisch“ bedeutet, dass es zwei komplexe Zahlen ω1,ω2 gibt, die keine reellen Vielfachen voneinander sind, so dass … Deutsch Wikipedia
elliptische Funktionen — ellịptische Funktionen, meromorphe Funktionen, die doppeltperiodisch sind, d. h., die den Funktionalgleichungen f (z + p1) = f (z) und f (z + p2) = f … Universal-Lexikon
Weierstraßsche elliptische Funktion — Im mathematischen Teilgebiet der Funktionentheorie sind elliptische Funktionen doppeltperiodische meromorphe Funktionen. „Doppeltperiodisch“ bedeutet, dass es zwei komplexe Zahlen ω1,ω2 gibt, die keine reellen Vielfachen voneinander sind, so dass … Deutsch Wikipedia
Jacobische elliptische Funktion — In der Mathematik ist eine Jacobische elliptische Funktion eine von zwölf speziellen elliptischen Funktionen. Die Jacobischen elliptischen Funktionen haben einige Analogien zu den trigonometrischen Funktionen und finden zahlreiche Anwendungen in… … Deutsch Wikipedia
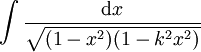
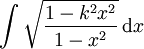
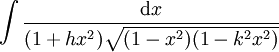
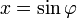 werden diese Integrale auf die Legendre-Form gebracht:
werden diese Integrale auf die Legendre-Form gebracht: