Hyperbel (Mathematik)

Hyperbel in der Architektur: Kathedrale von Brasilia

In der ebenen Geometrie versteht man unter einer Hyperbel eine spezielle Kurve, die aus zwei zueinander symmetrischen, sich ins Unendliche erstreckenden Ästen besteht. Sie zählt neben dem Punkt, dem Kreis, der Parabel und der Ellipse zu den Kegelschnitten. Ihre Exzentrizität ist größer als Eins.

Die Hyperbel wurde von Menaichmos entdeckt. Die von Apollonios von Perge eingeführte Bezeichnung kommt aus dem Griechischen und bezieht sich auf die Übertreibung (ὑπερβολή, hyperbolé, von altgriechisch βάλλειν bállein „werfen“, ὑπερβάλλειν hyperballein „über das Ziel hinaus werfen“) des Schnittwinkels (oder der numerischen Exzentrizität ε) beim Kegelschnitt: Mit steigendem Schnittwinkel verwandelt sich der Kreis (ε = 0) erst zu immer länglicheren Ellipsen und dann über die Parabel (ε ist 1 und die schneidende Ebene parallel zu einer Tangentialebene des Kegels) zu Hyperbeln mit ε > 1.^[1]

Definitionen und Begriffe

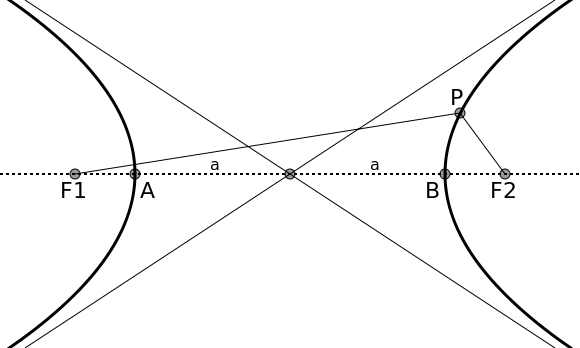
Eine Hyperbel ist auch definiert als die Menge aller Punkte der Zeichenebene, für die die absolute Differenz der Abstände zu zwei gegebenen Punkten auf der Hauptachse, den so genannten Brennpunkten F₁ und F₂, konstant gleich 2a ist:

$hyp = \left\{P\mid \left|\overline{PF_1} - \overline{PF_2} \right| = 2a \right\}$

wobei a, auch reelle Halbachse genannt, der Abstand der Scheitel A und B vom Mittelpunkt der Hyperbel ist. Der Abstand der Brennpunkte vom Mittelpunkt heißt Brennweite oder lineare Exzentrizität und wird üblicherweise mit e bezeichnet. Die in der Einleitung erwähnte, dimensionslose numerische Exzentrizität ε ist e/a. Motiviert durch die Formel $\sqrt{a^2-b^2}$ für die Exzentrizität einer Ellipse mit den Halbachsen a und b definiert man für die Hyperbel eine imaginäre Halbachse $b = \sqrt{e^2-a^2}$, sodass a² + b² = e² gilt. Das abweichende Vorzeichen ist der Grund für die Bezeichnung imaginäre Achse oder auch Nebenachse für die Senkrechte durch den Mittelpunkt zur reellen Hauptachse.

Die halbe Länge einer Hyperbelsehne, die durch einen Brennpunkt geht und zur Hauptachse senkrecht verläuft, nennt man den Halbparameter (manchmal auch Quermaß oder nur Parameter) p der Hyperbel. p lässt sich berechnen durch

$p = \frac{b^2}a.$

Eigenschaften

Jede Hyperbel besitzt zwei Asymptoten, also zwei Geraden, denen sich die Punkte der Kurve beliebig annähern. Die beiden Asymptoten verlaufen durch den Mittelpunkt der Hyperbel. Ihr Schnittwinkel α gegenüber der Hauptachse ist gegeben durch $\tan\alpha = \tfrac ba$. Ist die Hyperbel gleichseitig, so stehen die Asymptoten senkrecht aufeinander.

Mit dem Begriff Direktrix oder Leitlinie bezeichnet man die beiden Parallelen zur Nebenachse im Abstand $d = \tfrac{a^2}e$. Für einen beliebigen Punkt X der Hyperbel ist das Verhältnis zwischen den Abständen zu einem Brennpunkt und zur zugehörigen Direktrix gleich der numerischen Exzentrizität:

$\frac{\overline{XF_1}}{\overline{XP_1}} = \frac{\overline{XF_2}}{\overline{XP_2}} = \varepsilon.$

Umgekehrt kann man einen Punkt (als Brennpunkt) und eine Gerade (als Direktrix) sowie eine reelle Zahl ε mit ε > 1 vorgeben und eine Hyperbel definieren als Menge aller Punkte der Ebene, für die das Verhältnis der Abstände zu dem Punkt und zu der Geraden gleich ε ist.

Gleichung der Hyperbel

Die Gleichung der Hyperbel erhält eine besonders einfache Form, wenn sie in "1.Hauptlage" liegt, das heißt, dass die beiden Brennpunkte auf der x-Achse symmetrisch zum Ursprung liegen; bei einer Hyperbel in 1.Hauptlage haben also die Brennpunkte die Koordinaten (e,0) und ( − e,0), und die Scheitel haben die Koordinaten (a,0) und ( − a,0).

Für einen beliebigen Punkt (x,y) in der Ebene nennen wir die Geraden durch den Punkt und jeweils einen Brennpunkt Leitstrahl des Punktes. Für den Punkt ist der Abstand zum Brennpunkt (e,0) – entlang dem einen Leitstrahl – gleich $\sqrt{ (x-e)^2 + y^2 }$, zum anderen Brennpunkt – entlang dem anderen Leitstrahl – $\sqrt{ (x+e)^2 + y^2 }$. Der Punkt (x,y) liegt also genau dann auf der Hyperbel, wenn die Differenz dieser beiden Ausdrücke gleich 2a oder gleich − 2a ist.

Durch algebraische Umformungen (unter Berücksichtigung von a² + b² = e²) kann man zeigen, dass die Gleichung

$\sqrt{(x-e)^2 + y^2} - \sqrt{(x+e)^2 + y^2} = \pm 2a$

zur Gleichung

$\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1$

äquivalent ist. Letztere Gleichung nennt man die Gleichung der Hyperbel in 1.Hauptlage.

Daraus ergibt sich, dass jede Hyperbel nach einer geeigneten Koordinatentransformation durch

$t \mapsto (a \cosh t, b \sinh t)$

parametrisiert werden kann. (Siehe auch cosh, sinh, Kreis- und Hyperbelfunktionen.)

Andere Lage

Kehrwertfunktion

Eine besonders einfach visualisierbare Hyperbel wird durch die Funktion $f(x) = \tfrac 1x$ beschrieben (siehe Abbildung). Für diese Hyperbel ist $a = b = \sqrt 2$, also e = 2, ihre Hauptachse ist die Gerade f(x) = x, ihre Scheitel sind die Punkte (1,1) und (-1,-1) und ihre Brennpunkte liegen bei $(\sqrt 2, \sqrt 2)$ und $(-\sqrt 2, -\sqrt 2)$.

Auch andere gebrochenrationale Funktionen, wie etwa $f(x)=\tfrac{2x+1}{3x-5}$, stellen Hyperbeln dar, sofern sie (mit Vielfachheit) genau eine Polstelle besitzen.

Formelsammlung

Hyperbelgleichung

Die allgemeine Hyperbel mit Mittelpunkt (0|0) erfüllt die Gleichung

x^TAx + c = 0

mit $x = (x,y)^T \in \mathbb{R}^2$ und einer symmetrischen 2x2 Matrix A, deren Eigenwerte verschiedene Vorzeichen haben und nicht verschwinden.

Der Spezialfall dieser Gleichung zur Diagonalmatrix $A = \operatorname{diag} \left(\frac{1}{\left|a\right|},-\frac{1}{\left|b\right|}\right)$ und c = -1 lautet

$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1.$

Das entspricht im Wesentlichen der Wahl der Hauptachsen der Hyperbel als x- und y-Achse.

Die Asymptoten der zugehörigen Hyperbeln sind die Geraden:

$y = \pm \frac ba x.$

Lage der Brennpunkte:

$(\pm~\sqrt{a^2 + b^2}, 0).$

Durch eine Verschiebung der Punkte mit T_m(x) = x + m um einen Vektor m = (x₀,y₀)^T erhält man Gleichungen für Hyperbeln mit Mittelpunkt (x₀,y₀) (wobei x' = T(x)):

0 = (T ^{− 1}(x'))^TAT ^{− 1}(x') = x'^TAx' − 2m^TAx' + m^TAm + c

oder allgemein (b = 2Am, d = m^T A m + c)

x'^TAx' + b^Tx' + d = 0

und im Spezialfall

$\frac{(x-x_0)^2}{a^2} - \frac{(y-y_0)^2}{b^2} = 1.$

Hyperbelgleichung (Parameterform)

Mittelpunkt (0|0), Hauptachse als x-Achse:

$\left\{\begin{matrix} x \, = \, \frac{a}{\cos t} \\ y \, = \, b \ \tan t \end{matrix}\right. \ , \ 0 \le t < 2\pi; \; t \ne \frac{\pi}{2}; \; t \ne \frac{3}{2}\pi$

Mittelpunkt (x₀ | y₀), Hauptachse parallel zur x-Achse:

$\left\{\begin{matrix} x = x_0 + \frac{a}{\cos t} \\ y = y_0 + b \ \tan t \end{matrix}\right. \ , \ 0 \le t < 2\pi; \; t \ne \frac{\pi}{2}; \; t \ne \frac{3}{2}\pi$

Hyperbelgleichung (Polarkoordinaten)

Winkel zur Hauptachse, Pol im Zentrum:

$r = \frac{b}{\sqrt{\varepsilon^2 \cos^2 \varphi - 1}}$

Pol in einem Brennpunkt:

$r = \frac{p}{1 \pm \varepsilon \cos \varphi}$

Tangentengleichung (kartesische Koordinaten)

Mittelpunkt (0|0), Hauptachse als x-Achse, Berührpunkt (x_B | y_B)

$\frac{x_B x}{a^2} - \frac{y_B y}{b^2} = 1$

Mittelpunkt (x₀ | y₀), Hauptachse parallel zur x-Achse, Berührpunkt (x_B | y_B)

$\frac{(x_B - x_0) (x - x_0)}{a^2} - \frac{(y_B - y_0) (y - y_0)}{b^2} = 1$

Weblinks

• Eric W. Weisstein: Hyperbola. In: MathWorld. (englisch)
• Hyperbola. In: MacTutor History of Mathematics archive (englisch)
• Berechnungen zu Hyperbeln (Javascript)

Einzelnachweise

1. ↑ I. N. Bronstein, K. A. Semendjajew (Begründer), Günter Grosche (Bearb.), Eberhard Zeidler (Hrsg.): Teubner-Taschenbuch der Mathematik. Teubner, Stuttgart 1996, ISBN 3-8154-2001-6, S. 24.