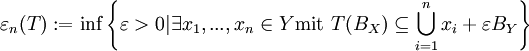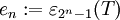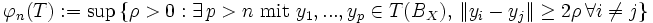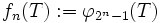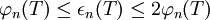Entropiezahlen

Entropiezahlen sind in der Funktionalanalysis Kennzahlen von stetigen linearen Operatoren. Das Konzept basiert auf dem Begriff der Epsilon-Entropie.

Definition

Äußere Entropiezahlen

Seien X und Y Banachräume und T ein linearer stetiger Operator 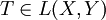$T \in L(X, Y )$, so nennt man

$\varepsilon_n(T) := \inf \left\{\varepsilon > 0|\exists x_1, ..., x_n \in Y \mbox{mit }T(B_X)\subseteq\bigcup_{i=1}^n{{x_i} + \varepsilon B_Y }\right\}$

n-te Entropiezahl von T, wobei B_X bzw. B_Y die abgeschlossenen Einheitskugeln in X bzw. Y sind. Wir nennen

$e_n := \varepsilon_{2^n-1}(T)$

die n-te dyadische Entropiezahl von T.

Beim ¨Ubergang von den “normalen“ Entropiezahlen zu den dyadischen gehen bei der asymptotischen Betrachtung keine wesentlichen Informationen verloren. Darum werden die dyadischen Entropiezahlen auch oft nur Entropiezahlen genannt.

Innere Entropiezahlen

Seien X und Y Banachräume und T ein linearer stetiger Operator 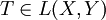$T \in L(X, Y )$, so nennt man

$\varphi_n(T):=\sup\left\{\rho>0: \exists\, p>n\mbox{ mit }y_1,...,y_p\in T(B_X),\, \left\|y_i-y_j\right\|\geq2\rho\,\forall i\neq j\right\}$

innere Entropiezahl von T.

$f_n(T):=\varphi_{2^n-1}(T)$

wird dyadische innere Entropiezahl von T genannt.

Zusammenhang von inneren zu äußeren Entropiezahlen

Wie Carl und Stephani in ihrem Buch Entropy, compactness and the approximation of operators gezeigt haben, besteht die Beziehung

$\varphi_n(T)\leq\epsilon_n(T)\leq2\varphi_n(T)$

weshalb man meist nur e_n(T) betrachtet.

Bemerkung

Wenn man auf die Definition der Entropiezahlen sieht, erkennt man folgenden elementaren Zusammenhang:

T ist kompakt $\Leftrightarrow e_n(T)\rightarrow0.$

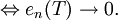
Auf Grund dieser Tatsache kann man die Entropiezahlen nutzen um dem Operator einen "Grad der Kompaktheit" zuzuordnen, d.h. je schneller die Entropiezahlen gegen 0 fallen, umso kompakter ist der Operator.

Literatur

• Hermann König: Eigenvalue Distribution of Compact Operators, Birkhäuser, 1985 (enthält eine gute Einführung in die Theorie der s-Zahlen)
• David Eric Edmunds & Hans Triebel: Function Spaces, Entropy Numbers, Differential Operators, Cambridge University Press, 1994
• Bernd Carl & Irmtraud Stephani Entropy, compactness and the approximation of operators, Cambridge University Press, 1990