Ertragsfunktion

Das Ertragsgesetz ist ein Modell aus der Volkswirtschaftslehre. Es beschreibt die Effizienz eines Wertschöpfungsprozesses, wenn nur ein variabler Produktionsfaktor erhöht wird, die anderen aber gleich bleiben (ceteris paribus). Damit bietet dieses Modell ein besonders anschauliches (didaktisches) Konzept, Relationen von Einsatz (Input) und Ertrag (Output) zu beschreiben. In der Praxis sind solche Relationen durch nicht orthogonale Parameter bestimmt, deren gegenseitiger Einfluss nicht völlig zu trennen ist.

Zwei besondere Ertragsgesetze sind benannt: das klassische Ertragsgesetz und das neoklassische Ertragsgesetz. Beides sind eher qualitative Beschreibungsfunktionen, an denen verschiedene Merkmale diskutiert werden. Das Ertragsgesetz ist weder eine Regel im Sinne einer juristischen Norm noch bezeichnet es eine Regel im Sinne einer unbedingten wissenschaftlichen Methode.

Das klassische Ertragsgesetz gilt als älteste Produktionsfunktion. Als seine „Entdecker“ gelten unabhängig voneinander Turgot, Stewart und Johann Heinrich von Thünen, die aus verschiedenen Ansätzen heraus zu vergleichbaren Beschreibungen kamen.

Das neoklassische Ertragsgesetz, auch als das Gesetz vom abnehmenden Grenzertrag bezeichnet, zeigt anders als das klassische Ertragsgesetz keine ansteigende Grenzrate in der ersten Phase, wie sie häufig bei einer landwirtschaftlichen Produktion auftritt.

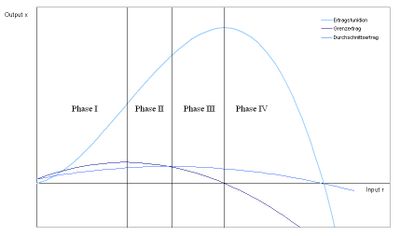
In der diagrammatischen Darstellung erinnert es an die Gestalt eines nach rechts geneigten S. In der Betriebswirtschaftslehre ist der Verlauf auch als ertragsgesetzliche Produktionsfunktion oder Produktionsfunktion vom Typ A bekannt. Der Mehreinsatz eines Produktionsmittels bei Konstanz der übrigen Produktionsfaktoren bringt zuerst zunehmende Ertragszuwächse (Grenzerträge oder Grenzprodukte), dann von einer bestimmten Einsatzmenge an abnehmende und schließlich sogar negative Grenzerträge.

Definition

Ertrag ist das Funktional der Ausbringung (Output) über dem Einsatz (Input). Grenzertrag ist das (erste) Differential des Ertrags nach dem Einsatz. Durchschnittsertrag ist der gleitende Mittelwert des (spezifischen) Ertrags.

Phasen

Phasen des Ertragsgesetzes

Plausibilität besitzt das klassische Ertragsgesetz über seinen gesamten Verlauf (eigentlich nur) für landwirtschaftliche Produktionsprozesse bei partieller Faktorvariation. Gleichwohl wird es ebenso als Ertragskurve bei totaler Faktorvariation und für andere Produktionsprozesse herangezogen. Der Grund dafür ist sein hohes didaktisches Potential. Das Funktional zeigt sowohl Bereiche zu- als auch abnehmender Grenzerträge. Die Stelle des Wechsels von zunehmenden zu abnehmenden Grenzerträgen (Wendepunkt) wird als (erste) „Schwelle“ bezeichnet, da ab diesem Punkt die Ertragszuwächse fallen. Mit dem Wendepunkt korrespondiert das Minimum der Grenzkosten, das als weitere (zweite) Schwelle bezeichnet wird. Beim klassischen Ertragsgesetz besitzen die durchschnittlichen Erträge dort ein Maximum, wo die Produktionselastizität eins ist, d. h. die Grenzerträge gleich den Durchschnittserträgen sind.

Phase I

Der erste Abschnitt ist durch eine überproportionale Steigung der Ertragsfunktion gekennzeichnet. Grenz- und Durchschnittsertrag steigen ebenfalls, jedoch ist die Phase I durch das Maximum der Grenzertragsfunktion begrenzt. Mathematisch ist dies zu ermitteln, indem man die 1. Ableitung gleich Null setzt

Phase II

Der zweite Abschnitt ist durch eine annähernd proportionale Steigung der Ertragsfunktion gekennzeichnet (verursacht durch annähernd konstante Grenzerträge). Die Grenzertragsfunktion sinkt bereits wieder, während die Durchschnittsertragsfunktion noch steigt. Phase II ist durch das Maximum der Durchschnittsertragsfunktion begrenzt. Mathematisch ist dies zu ermitteln, indem man den Durchschnittsertrag mit dem Grenzertrag gleichsetzt .

Phase III

Der dritte Abschnitt ist ebenfalls durch eine unterproportionale Steigung der Ertragsfunktion gekennzeichnet. In dieser Phase sinkt sowohl die Grenzertragsfunktion als auch die Durchschnittsertragsfunktion. Begrenzt ist die Phase III durch das Maximum der Ertragsfunktion. An dieser Intervallgrenze schneidet die Grenzertragsfunktion die Abszisse. Mathematisch lässt sich dies ermitteln, indem man die 1. Ableitung gleich Null setzt.

Phase IV

Im vierten Abschnitt weisen Ertrags-, Grenz- und Durchschnittsertragsfunktion eine negative Steigung auf.

Beispiel

In der Landwirtschaft lässt sich das funktional (auch nach dem französischen Ökonom J. Turgot und dessen Turgotschem Ertragsgesetz) am Beispiel der Verwendung von Dünger aufzeigen: Durch den kontinuierlich gesteigerten Gebrauch von Düngemitteln (bei sonst gleich bleibenden Ressourcen/Bedingungen (ceteris paribus), also z. B. gleichbleibender Fläche) wächst der Ertrag zunächst stetig an. Der Ertragszuwachs je zusätzlich ausgebrachter Düngemittelmenge nimmt ab einer bestimmten Ausbringungsmenge ab. Dies führt bei weiterer Düngerausbringung schließlich sogar zu einer Gesamtertragsminderung und sogar zur Bodenvergiftung: Ein überhöhter Einsatz von Düngemitteln wird den Ertrag unter das Niveau führen, das ohne Düngemittel erreicht worden wäre und schließlich jeden Ertrag vernichten. Ähnliche Beobachtungen können auch bei den Faktoren Wärme und Wasser gemacht werden.

Diese Beobachtungen gehen auch auf Eilhard Alfred Mitscherlich zurück, der Das Gesetz vom Minimum und das Gesetz des abnehmenden Bodenertrages mit entsprechenden Verlaufsdiagrammen im Jahre 1909 publizierte.

Am Beispiel der industriellen Produktion oder in der Verwaltung lässt sich das Ertragsgesetz auf den gesteigerten Einsatz von Personal bei sonst gleich bleibenden Rahmenbedingungen ebenfalls beobachten: Je größer die Anzahl von Mitarbeitern ist, desto größer ist der Kommunikations- und Abstimmungsbedarf. Es können jedoch Situationen erreicht werden, wo sich Mitarbeiter gegenseitig nur noch im Weg stehen oder sich demotivieren. Mehr bewegt wird allein durch die Personalvermehrung also nicht. Ein Staat, der seine Wirtschaft zentralistisch steuert und Arbeitnehmer den Produktionsanlagen zuteilt, um so das Problem der Arbeitslosigkeit zu vermeiden, kann seine Produktivität auf diese Art kaum steigern.

Das klassische Ertragsgesetz ist nicht notwendig für die Begründung eines (kurzfristigen) ertragsgesetzlichen Kostenverlaufs, der zu u-förmigen Durchschnittskostenverläufen führt. Diese können auch bei durchgängig abnehmenden Ertragszuwächsen als Folge des Zusammenspiels von steigenden Grenz- und sinkenden durchschnittlichen Fixkosten auftreten.

Weblinks

• Die zwei Seiten des Spiegels

Dieser Text basiert ganz oder teilweise auf dem Mikroökonomie-Glossar von Professor Wilhelm Lorenz und ist unter GNU-FDL lizenziert.