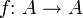- Extensivität
-
Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!
Extensivität bezeichnet in der Mathematik die Eigenschaft einer Abbildung, Mengen „zu vergrößern“. Entsprechend „verkleinern“ intensive (auch anti-extensive) Abbildungen Mengen.
Inhaltsverzeichnis
Definition
Sei
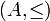 eine teilweise geordnete Menge. Eine Abbildung
eine teilweise geordnete Menge. Eine Abbildungheißt extensiv, falls gilt:
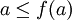 für alle
für alle 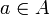 .
.
Sie heißt intensiv, falls gilt:
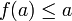 für alle
für alle 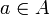 .
.
Beispiele
- Auf
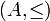 ist die Identität
ist die Identität 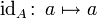 extensiv und intensiv, da
extensiv und intensiv, da 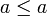 immer gilt.
immer gilt. - Definitionsgemäß sind Hüllenoperatoren extensiv und Kernoperatoren intensiv auf der Potenzmenge einer beliebigen Menge mit der mengentheoretischen Inklusion als Halbordnung.
Fixpunktsatz von Bourbaki-Kneser
Nach dem Fixpunktsatz von Bourbaki und Kneser besitzt jede extensive Abbildung
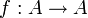 bereits dann einen Fixpunkt, falls A streng induktiv geordnet ist. Daraus lässt sich unter Zuhilfenahme des Auswahlaxioms das Lemma von Zorn beweisen.
bereits dann einen Fixpunkt, falls A streng induktiv geordnet ist. Daraus lässt sich unter Zuhilfenahme des Auswahlaxioms das Lemma von Zorn beweisen.Literatur
- Marcel Erné: Einführung in die Ordnungstheorie. Bibliographisches Institut, Mannheim 1982, ISBN 3-411-01638-8.
- H. Werner: Einführung in die allgemeine Algebra. Bibliographisches Institut, Mannheim 1978, ISBN 3-411-00120-8.
- S. Lang: Algebra. Addison-Wesley, 1993.
Wikimedia Foundation.