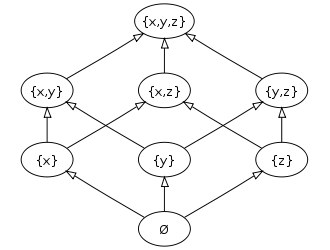
- Potenzmenge
-
Als Potenzmenge bezeichnet man in der Mengenlehre die Menge aller Teilmengen einer gegebenen Grundmenge. Die Potenzmenge ist also ein Mengensystem, das heißt, eine Menge, deren Elemente selbst Mengen sind. Man notiert die Potenzmenge von X meist als
 . In Formelschreibweise lautet die Definition
. In Formelschreibweise lautet die Definition (lies: P von X ist definiert als die Menge aller U, für die gilt: U ist Teilmenge von X).
(lies: P von X ist definiert als die Menge aller U, für die gilt: U ist Teilmenge von X).
Dabei ist zu beachten, dass die leere Menge
 Teilmenge einer jeden Menge ist. Andere gebräuchliche Notationen für die Potenzmenge sind:
Teilmenge einer jeden Menge ist. Andere gebräuchliche Notationen für die Potenzmenge sind:  .
.Das Wesen der Potenzmenge wurde schon von Ernst Zermelo untersucht. Der kompakte Begriff „Potenzmenge“ hingegen – der sich in dem Zusammenhang mit der arithmetischen Potenzoperation anbietet – wurde auch von Gerhard Hessenberg in seinem Lehrbuch von 1906 noch nicht benutzt; er verwendet dafür die Wortverbindung „Menge der Teilmengen“.
Inhaltsverzeichnis
Beispiele




Strukturen auf der Potenzmenge
Partielle Ordnung
Die Inklusionsrelation
 ist eine Halbordnung auf
ist eine Halbordnung auf  (und keine Totalordnung, wenn X mindestens zwei Elemente hat). Das kleinste Element der Ordnung ist
(und keine Totalordnung, wenn X mindestens zwei Elemente hat). Das kleinste Element der Ordnung ist  , das größte Element ist X.
, das größte Element ist X.Vollständiger Verband
Die Halbordnung
 ist ein vollständiger Verband. Dies bedeutet, dass es zu jeder Teilmenge von
ist ein vollständiger Verband. Dies bedeutet, dass es zu jeder Teilmenge von  ein Infimum und ein Supremum (in
ein Infimum und ein Supremum (in  ) gibt. Konkret ist für eine Menge
) gibt. Konkret ist für eine Menge  das Infimum von T gleich dem Durchschnitt der Elemente von T, und das Supremum von T ist gleich der Vereinigung der Elemente von T, also
das Infimum von T gleich dem Durchschnitt der Elemente von T, und das Supremum von T ist gleich der Vereinigung der Elemente von T, alsoDas größte und das kleinste Element erhält man als Infimum bzw. Supremum der leeren Menge, also
Boolescher Verband
Zieht man noch die Komplementabbildung
 heran, ist
heran, ist  ein boolescher Verband, also ein distributiver und komplementärer Verband.
ein boolescher Verband, also ein distributiver und komplementärer Verband.Kommutativer Ring
Jeder boolesche Verband induziert eindeutig eine kommutative Ringstruktur, den sogenannten booleschen Ring. Hier auf
 ist die Ringaddition gegeben durch die symmetrische Differenz von Mengen, die Ringmultiplikation ist der Durchschnitt. Die leere Menge ist neutral für die Addition und X ist neutral für die Multiplikation.
ist die Ringaddition gegeben durch die symmetrische Differenz von Mengen, die Ringmultiplikation ist der Durchschnitt. Die leere Menge ist neutral für die Addition und X ist neutral für die Multiplikation.Charakteristische Funktionen
Jeder Teilmenge
 kann man die charakteristische Funktion
kann man die charakteristische Funktion  zuordnen, wobei gilt
zuordnen, wobei giltDiese Zuordnung ist eine Bijektion zwischen
 und {0,1}X (wobei die Notation BA für die Menge aller Funktionen von A nach B benutzt wird). Dies motiviert für
und {0,1}X (wobei die Notation BA für die Menge aller Funktionen von A nach B benutzt wird). Dies motiviert für  auch die Schreibweise 2X, denn im von Neumanns Modell der natürlichen Zahlen ist 2 = {0,1} (allgemein: n = {0,...,n − 1}).
auch die Schreibweise 2X, denn im von Neumanns Modell der natürlichen Zahlen ist 2 = {0,1} (allgemein: n = {0,...,n − 1}).Die Korrespondenz
 ist zunächst eine reine Bijektion, lässt sich aber leicht als Isomorphismus bezüglich jeder der oben betrachteten Strukturen auf der Potenzmenge nachweisen.
ist zunächst eine reine Bijektion, lässt sich aber leicht als Isomorphismus bezüglich jeder der oben betrachteten Strukturen auf der Potenzmenge nachweisen.Die Größe der Potenzmenge (Kardinalität)
| M | bezeichnet die Mächtigkeit einer Menge M.
- Für endliche Mengen X gilt:
 .
.
- Für unendliche Mengen X gilt (Satz von Cantor):
 .
.
Der Übergang zur Potenzmenge liefert also immer eine größere Mächtigkeit. Analog zu endlichen Mengen schreibt man auch 2 | X | für
 von einer unendlichen Menge X. Die verallgemeinerte Kontinuumshypothese (GCH) besagt für unendliche Mengen X, dass
von einer unendlichen Menge X. Die verallgemeinerte Kontinuumshypothese (GCH) besagt für unendliche Mengen X, dass  die nach | X | nächstgrößere Mächtigkeit ist:
die nach | X | nächstgrößere Mächtigkeit ist:Beschränkung auf kleinere Teilmengen
Mit
 wird die Menge derjenigen Teilmengen von X bezeichnet, die weniger als κ Elemente enthalten. Beispielsweise ist
wird die Menge derjenigen Teilmengen von X bezeichnet, die weniger als κ Elemente enthalten. Beispielsweise ist  : Die Menge {a,b,c} selbst fehlt, da sie nicht weniger als 3 Elemente hat.
: Die Menge {a,b,c} selbst fehlt, da sie nicht weniger als 3 Elemente hat.Sonstiges
- Die Existenz der Potenzmenge zu jeder Menge wird in der Zermelo-Fraenkel-Mengenlehre als eigenes Axiom gefordert, nämlich durch das Potenzmengenaxiom.
- Eine Teilmenge der Potenzmenge heißt Mengensystem.
Literatur
- Oliver Deiser: Einführung in die Mengenlehre, Springer, 2004, ISBN 978-3-540-20401-5
Weblinks
Wikimedia Foundation.