Extrempunkt

Extrempunkt
Die Extrempunkte (Hoch- und Tiefpunkt) sowie Nullstellen, Wendepunkt und Wendetangente der Funktion f(x) = 0,5x3 + 3x3 + 3x − 2

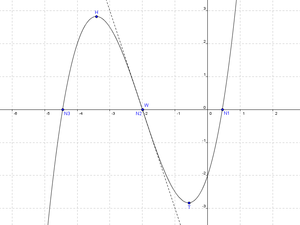
In der Mathematik ist ein Extrempunkt E\left(x_E|f(x_E)\right) ein Punkt auf einem Funktionsgraphen, so dass für alle x in einer kleinen Umgebung um xE gilt, dass f\left(x\right) nicht größer (Maximum) bzw. nicht kleiner (Minimum) als f\left(x_E\right) ist. Für stetig differenzierbare Funktionen in offenen Umgebungen heißen Punkte kritisch, wenn die Ableitung in diesem Punkt identisch 0 verschwindet. Extrempunkte werden in Hochpunkte und Tiefpunkte unterteilt. Die Ermittlung des Extremwerts, der diesen Extrempunkt ausmacht, ist Bestandteil einer Kurvendiskussion.

Es ist zu beachten, dass Extremwerte auch auf dem Rand des Definitionsbereichs auftreten können, ohne dass die Ableitung in diesem Punkt definiert oder 0 ist.


Wikimedia Foundation.

Игры ⚽ Нужна курсовая?

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Extrempunkt — ekstremumo taškas statusas T sritis Standartizacija ir metrologija apibrėžtis Funkcijos maksimumo arba minimumo taškas. atitikmenys: angl. extreme point vok. Extremalpunkt, m; Extrempunkt, m rus. точка экстремума, f; экстремальная точка, f pranc …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

  • Extrempunkt — ekstremumo taškas statusas T sritis fizika atitikmenys: angl. extreme point vok. Extremalpunkt, m; Extrempunkt, m rus. точка экстремума, f; экстремальная точка, f pranc. point extrême, m …   Fizikos terminų žodynas

  • Extrempunkt — Ex|t|rem|punkt, der (Math.): extremer Punkt einer Kurve (Minimum od. Maximum). * * * Ex|trem|punkt, der (Math.): extremer Punkt einer Kurve (Minimum od. Maximum) …   Universal-Lexikon

  • Kurvendiskussion — Unter Kurvendiskussion versteht man in der Mathematik die Untersuchung des Graphen einer Funktion auf dessen geometrische Eigenschaften, wie zum Beispiel Nullstellen, Hoch und Tiefpunkte, Wendepunkte, gegebenenfalls Sattel und Flachpunkte,… …   Deutsch Wikipedia

  • Extremstelle — Unter Kurvendiskussion versteht man in der Mathematik die Untersuchung des Graphen einer Funktion auf dessen Eigenschaften, wie zum Beispiel Nullstellen, Hoch und Tiefpunkte, Wendepunkte, Polstellen, Verhalten im Unendlichen usw. Die Ergebnisse… …   Deutsch Wikipedia

  • Extremwertproblem — Unter Kurvendiskussion versteht man in der Mathematik die Untersuchung des Graphen einer Funktion auf dessen Eigenschaften, wie zum Beispiel Nullstellen, Hoch und Tiefpunkte, Wendepunkte, Polstellen, Verhalten im Unendlichen usw. Die Ergebnisse… …   Deutsch Wikipedia

  • Funktionsuntersuchung — Unter Kurvendiskussion versteht man in der Mathematik die Untersuchung des Graphen einer Funktion auf dessen Eigenschaften, wie zum Beispiel Nullstellen, Hoch und Tiefpunkte, Wendepunkte, Polstellen, Verhalten im Unendlichen usw. Die Ergebnisse… …   Deutsch Wikipedia

  • Ganzrationale Funktion — Eine ganzrationale Funktion oder Polynomfunktion ist in der Mathematik eine Summe von Potenzfunktionen mit natürlichen Exponenten. Man kann also ihren Funktionsterm in folgende Form bringen: mit einer natürlichen Zahl n und reellen Zahlen , wobei …   Deutsch Wikipedia

  • Notwendige und hinreichende Bedingung — Notwendige Bedingung und hinreichende Bedingung sind Begriffe aus der Aussagenlogik und Kausalitätstheorie, welche die philosophische Bedingung genauer explizieren. Sie unterscheiden zwischen notwendigen und hinreichenden Typen von… …   Deutsch Wikipedia

  • Phelps'sches Theorem — Die Goldene Regel der Akkumulation von Edmund S. Phelps besagt, dass der Konsum je Kopf der Bevölkerung oder je Arbeitnehmer dann maximiert wird, wenn der Zinssatz gleich der Wachstumsrate des Bruttoinlandsprodukts ist. Die Herleitung dieser… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”