Funktionsgraph

Als Funktionsgraph, Graph (seltener: Funktionsgraf bzw. Graf), Kurve, Kurvenverlauf oder Plot einer Funktion f bezeichnet man in der Mathematik die Menge aller geordneten Paare (x, f(x)). Im allgemeinen Sprachgebrauch nennt man die grafische Darstellung dieser Menge, beispielsweise als Kurve in einem Koordinatensystem, ebenfalls Funktionsgraph.

Funktionsgraphen kann man mit Hilfe von Funktionenplottern auf den Computerbildschirm zeichnen lassen.

Zwei Beispiele für Funktionsgraphen:

Funktion	Graph	Anmerkung
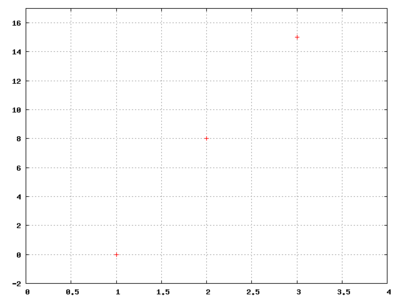
$f(x) = \begin{cases} 0 & \mbox{falls }x=1 \\ 8 & \mbox{falls }x=2 \\ 15 & \mbox{falls }x=3 \end{cases}$		Da der Definitionsbereich die Menge {1,2,3} ist, besteht der Graph nur aus den drei Punkten (1,0), (2,8) und (3,15).
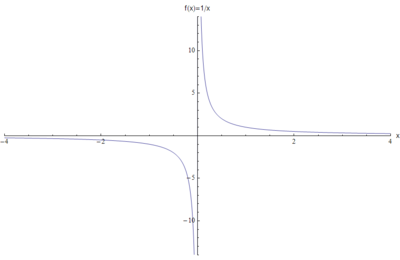
$f(x)=\frac{1}{x}$	Kehrwertfunktion	Für x = 0 ist diese Funktion nicht definiert. Deshalb gibt es auch keinen Punkt des Funktionsgraphen mit der x-Koordinate 0.

Formale Definition

Der Graph einer Funktion f mit der Definitionsmenge A ist die Menge

$\Gamma_f = \{(x, f(x)) | x \in A\}$

Der Graph ist eine Teilmenge von $A \times B$, wobei B die Zielmenge der Funktion ist.

Besondere Funktionsgraphen

Im kartesischen Koordinatensystem gilt:

• Lineare Funktionen haben als Graph eine Gerade.
• Der Graph einer quadratischen Funktion ist immer eine Parabel.

Graphen unstetiger Funktionen, Definitionslücken

Der Funktionswert der Signumfunktion an der Stelle 0 ist 0.

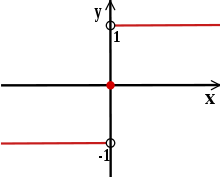
In der Darstellung der Graphen von unstetigen Funktionen oder von Funktionen mit Definitionslücken wird häufig durch $\bullet$ angedeutet, dass ein Punkt zum Graph gehört, und durch $\circ$, dass ein Punkt nicht Teil des Graphen ist. Ein Beispiel ist die Illustration der Signum-Funktion.

Siehe auch

• Quadrant

Weblinks

• FooPlot Online-Funktionsplotter (2-D und 3-D)
• Funktionsgraphen online zeichnen
• Funktionsplotter