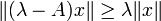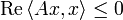- Akkretiver Operator
-
Dissipative Operatoren sind lineare Operatoren, die auf reellen oder komplexen Banachräumen definiert sind und gewisse Normabschätzungen erfüllen. Durch den Satz von Lumer-Phillips spielen sie eine wichtige Rolle bei der Betrachtung stark stetiger Halbgruppen.
Inhaltsverzeichnis
Definition
Seien X ein Banachraum und
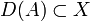 . Ein linearer Operator
. Ein linearer Operator 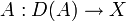 mit
mitfür alle λ > 0 und
 wird dissipativ genannt. Diese Bezeichnung geht auf Ralph Phillips zurück.
wird dissipativ genannt. Diese Bezeichnung geht auf Ralph Phillips zurück.Ist A ein linearer Operator und − A dissipativ, so wird A akkretiv genannt. Diese Bezeichnung wurde von Tosio Kato und Kurt Friedrichs eingeführt.
Hilbertraum
Wenn X ein Hilbertraum ist, ist ein linearer Operator
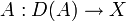 genau dann dissipativ, falls
genau dann dissipativ, fallsfür alle
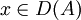 gilt, wobei
gilt, wobei 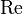 den Realteil bezeichnet.
den Realteil bezeichnet.Folgerungen
Sei (A,D(A)) ein dissipativer Operator auf einem Banachraum X.
- λ − A ist für ein λ > 0 surjektiv genau dann, wenn λ − A für alle λ > 0 surjektiv ist.
- A ist abgeschlossen genau dann, wenn das Bild von λ − A für ein λ > 0 abgeschlossen ist.
Beispiel
Betrachtet man auf einem beschränkten Gebiet
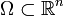 den Laplace-Operator Δ mit Dirichlet-Randbedingung auf L2(Ω) (siehe Lp-Raum), also
den Laplace-Operator Δ mit Dirichlet-Randbedingung auf L2(Ω) (siehe Lp-Raum), also 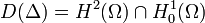 , erhält man:
, erhält man: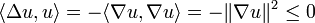 .
.
Wikimedia Foundation.