Fagnano-Problem

Höhenfußpunktdreieck: $\triangle DEF$
einbeschriebene Dreiecke: $\triangle DEF\,,\triangle GHI$
$|DE|+|EF|+|FD|\leq |GH|+|HI|+|IG|$

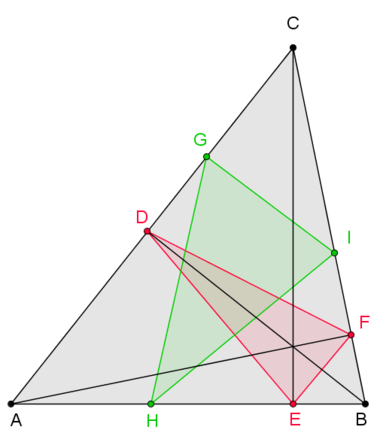
Das Fagnano-Problem ist ein nach Giovanni Fagnano benanntes Optimierungsproblem.

Bestimme das in ein spitzwinkliges Dreieck einbeschriebene Dreieck minimalen Umfangs.

Hierbei versteht man unter einem einbeschriebenen Dreieck eines Dreiecks $\triangle ABC$ ein Dreieck $\triangle GHI$, dessen Ecken auf den Seiten Dreiecks $\triangle ABC$ liegen, das heißt $G \in \overline{AC}$,$H \in \overline{AB}$ und $I \in \overline{BC}$. Für das Höhenfußpunktdreieck $\triangle DEF$ gilt, dass sein Umfang geringer ist als der eines jeden anderen einbschriebenen Dreiecks $\triangle GHI$ und somit ist es die Lösung des Fagnano-Problems.

Zunächst zeigte Giovanni Fagnanos Vater Giulio Carlo Fagnano, dass man zu einem beliebigen festen Punkt U auf $\overline{AB}$ 2 Punkte V auf $\overline{AC}$ und W auf $\overline{BC}$ so konstruieren kann, dass der Umfang des Dreieckes $\triangle UVW$ minimal ist. Giovanni Fagnano verwandte dieses Resultat, um dann mit Hilfe der Differentialrechnung von allen möglichen U auf $\overline{AB}$, dasjenige zu bestimmen für das der Umfang des Dreieckes $\triangle UVW$ minimal wird. Später wurden auch mehrere elementargeometrische Beweise gefunden, unter Anderem auch von Leopold Fejér und Hermann Amandus Schwarz. Diese Beweise verwenden meist Eigenschaften von Spiegelungen zur Bestimmung eines minimalen Weges.

Literatur

• Heinrich Dörrie: Triumph der Mathematik : 100 berühmte Probleme aus 2 Jahrtausenden mathemat. Kultur. F. Hirt 1940, Problem 90
• Paul J. Nahin: When Least is Best: How Mathematicians Discovered Many Clever Ways to Make Things as Small (or as Large) as Possible. Princeton University Press 2004, ISBN 0691070784, S. 67
• Coxeter, H. S. M., und S. L. Greitzer: Zeitlose Geometrie, Klett Stuttgart, 1983

Weblinks

• Wolfgang Zimmer: Eine offene Aufgabe zum Thema „Minimale Entfernungen“ (Sinus Materialien) (PDF-Datei; 141 kB)
• Fagnano-Problem auf cut-the-knot (engl.)
• Fagnano-Problem in der Encyclopaedia of Mathematics (engl.)
• Fagnano-Problem auf einer Webseite zur Dreiecksgemometrie (engl.)
• Eric W. Weisstein: Fagnano's problem. In: MathWorld. (englisch)