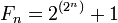Fermatzahlen

Eine Fermat-Zahl, benannt nach dem französischen Mathematiker Pierre de Fermat, ist eine Zahl der Form

$F_n = 2^{(2^n)} + 1$

wobei n eine natürliche Zahl ist. Die ersten Fermat-Zahlen sind

3, 5, 17, 257, 65537, … (Folge A000215 in OEIS)

Eine Fermat-Zahl, die gleichzeitig Primzahl ist, wird Fermat'sche Primzahl genannt. Fermat zeigte, dass die ersten fünf Fermat-Zahlen Primzahlen sind und vermutete 1637, dass dies auf alle Fermat-Zahlen zutrifft. Diese Vermutung wurde von Leonhard Euler 1732 widerlegt, indem er mit 641 einen echten Teiler von F₅ = 4294967297 berechnete. Man vermutet inzwischen, dass alle Fermat-Zahlen, außer den ersten fünf, keine Primzahlen sind. Diese umgekehrte Vermutung beruht auf dem Primzahlsatz, wonach die Anzahl der Primzahlen kleiner oder gleich x näherungsweise x / ln(x) beträgt. Die Primzahlendichte oder "Wahrscheinlichkeit" dafür, dass F_n eine Primzahl ist, beträgt daher näherungsweise 1,44/2ⁿ. Die Summe dieser Ausdrücke ist eine geometrische Reihe und für alle weder teilweise noch vollständig faktorisierten Fermat-Zahlen sehr gering.

Wenn 2ⁿ + 1 eine Primzahl ist, dann ist notwendig n eine Zweierpotenz: Ist n = ab mit 1 < a,b < n und ungeradem b, dann ist

2ⁿ + 1 ≡ (2^a)^b + 1 ≡ (−1)^b + 1 ≡ 0 (mod 2^a + 1).

Wenn also n einen ungeraden Teiler hat, dann ist 2ⁿ + 1 zusammengesetzt. Mit anderen Worten, für jede Primzahl der Form 2ⁿ + 1 ist n eine Zweierpotenz und die Primzahl 2ⁿ + 1 ist eine Fermat'sche Primzahl. Dies gilt auch für verallgemeinerte Fermat'schen Zahlen (siehe unten).

Faktorisierungsstatus von Fermat-Zahlen

Die Zahlen F₀ bis F₄ sind Primzahlen.

Die vollständig faktorisierten Fermat-Zahlen entnimmt man folgender Tabelle:

Von F₅ bis F₇:

n	Fn	Entdecker der Faktoren
5	641 · 6700417	Euler (1732)
6	274177 · 67280421310721	Landry & Le Lasseur (1880)
7	59649589127497217 · 5704689200685129054721	Morrison & Brillhart (1970)

Ab F₈

n	Entdecker der Faktoren
8	Brent & Pollard (1980)
9	Western (1903), Lenstra & Lenstra & Manasse & Pollard (1990)
10	Selfridge (1953), Brillhart (1962), Brent (1995)
11	Cunningham (1899), Brent & Morain (1988)

Von den Zahlen F₁₂ bis F₃₂, sowie von etlichen größeren Fermat-Zahlen ist bekannt, dass sie zusammengesetzt sind, hauptsächlich weil ein oder mehrere Faktoren gefunden wurden. Von vier Fermat-Zahlen (F₁₄, F₂₀, F₂₂ und F₂₄) kennt man allerdings keinen Faktor, hat aber gezeigt, dass sie zusammengesetzt sind. Die kleinste Fermat-Zahl, von der nicht bekannt ist, ob sie prim oder zusammengesetzt ist, ist F₃₃; die größte, von der ein Faktor bekannt ist, ist F_2478782, deren Faktor 3 * 2^2478785 + 1 wurde 2003 von Cosgrave, Jobling, Woltman und Gallot entdeckt. Insgesamt weiß man von 230 Fermat-Zahlen, dass sie zusammengesetzt sind.^[1]

Um von einer Fermat-Zahl nachzuweisen, dass sie zusammengesetzt ist, benutzt man in der Regel den Pepin-Test und den Suyama-Test, die beide besonders auf diese Zahl zugeschnitten und sehr schnell sind.

Eigenschaften

• Für einen Teiler p einer Fermat-Zahl F_n, n ≥ 5, gilt p ≡ 1 (mod 2ⁿ⁺²); (z. B. Faktor 641 von F₅: 641 = 2⁷*5 +1 = 128*5 +1)

• Fermat-Zahlen lassen sich rekursiv berechnen aus

F_n = F₀F₁...F_n-1 + 2

• Je zwei Fermat-Zahlen sind zueinander teilerfremd, wie aus der letzten Aussage folgt. Daraus lässt sich schließen, dass es unendlich viele Primzahlen gibt (siehe auch Beweisarchiv).

Geometrische Anwendung der Fermat'schen Primzahlen

Carl Friedrich Gauß zeigte (Erstveröffentlichung von Pierre Wantzel im Jahre 1837), dass es einen Zusammenhang zwischen der Konstruktion von regelmäßigen Vielecken und den Fermat'schen Primzahlen gibt: Ein regelmäßiges Vieleck mit n Seiten kann dann und nur dann mit Zirkel und Lineal konstruiert werden, wenn n eine Potenz von 2 oder das Produkt einer Potenz von 2 und verschiedenen Fermat'schen Primzahlen ist ^[2]. Insbesondere zeigte Gauß so die Konstruierbarkeit des regelmäßigen Siebzehnecks.

Verallgemeinerte Fermat'sche Zahlen

Statt der Basis 2 kann man auch eine andere Basis wählen. Eine Zahl der Form 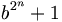$b^{2^n}+1$, mit einer natürlichen Zahl b heißt Verallgemeinerte Fermat'sche Zahl. Ist eine solche Zahl auch noch prim, dann heißt sie Verallgemeinerte Fermat'sche Primzahl.

Beispiel: b=6, n=2 ergibt die Primzahl 6⁴ + 1 = 1297.

Die größte bekannte verallgemeinerte Fermat'sche Primzahl ist derzeit die im März 2008 veröffentlichte Primzahl 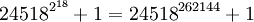$24518^{2^{18}}+1=24518^{262144}+1$ mit 1150678 Ziffern.^[3]

Die zweit größte bekannte verallgemeinerte Fermat'sche Primzahl ist die 2003 entdeckte Primzahl 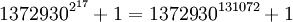$1372930^{2^{17}}+1=1372930^{131072}+1$ mit 804474 Ziffern.^[4] Beide Primzahlen wurden vom Projekt Generalized Fermat Prime Search^[5] entdeckt, das große verallgemeinerte Fermat'sche Primzahlen sucht.

Die meisten der oben genannten Ergebnisse konnten natürlich nur mit Computerhilfe gefunden werden.

Siehe auch

• Mersenne-Primzahlen
• Prothsche Primzahl

Einzelnachweise

1. ↑ Aktueller Faktorisierungsstatus aller Fermatzahlen (englisch) (3. Aug. 2007)
2. ↑ Emil Artin: Galoissche Theorie. Verlag Harri Deutsch, Zürich 1973, ISBN 3-87144-167-8, S 85.
3. ↑ http://primes.utm.edu/primes/lists/short.txt The largest known primes (26. März 2008: Rangplatz 13)
4. ↑ http://primes.utm.edu/primes/lists/short.txt Short list of largest known primes (Rangplatz 22 am 26. März 2008)
5. ↑ http://perso.wanadoo.fr/yves.gallot/primes/index.html GFPS Internationale Suche nach Verallgemeinerten Fermatschen Primzahlen (englisch)

Weblinks

• http://www.fermatsearch.org Distributed Search for Fermat Number Divisors (englisch)
• http://mathworld.wolfram.com/FermatNumber.html (englisch)