- Fisher-Matrix
-
Die Fisher-Information ist eine Kenngröße aus der mathematischen Statistik und der Informationstheorie, die für eine Familie von Wahrscheinlichkeitsdichten definiert werden kann und Aussagen über die bestmögliche Qualität von Parameterschätzungen in diesem Modell liefert. Sie ist nach dem Mathematiker und Statistiker Ronald Fisher benannt.
Definition
Falls das zu Grunde liegende Modell aus einer Familie
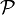 von Wahrscheinlichkeitsdichten
von Wahrscheinlichkeitsdichten 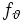 mit unbekanntem Parameter
mit unbekanntem Parameter 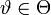 besteht, so ist die Fisher-Information für Zufallsvariablen
besteht, so ist die Fisher-Information für Zufallsvariablen 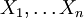 als
alsdefiniert.
Eigenschaften und Anwendungen
Die Fisher-Information ist unter der Regularitätsbedingung
additiv, d. h. für unabhängige Zufallsvariablen
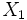 und
und 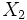 gilt
gilt 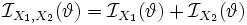 . Diese Eigenschaft ist eine einfache Anwendung der Tatsache, dass sich die Varianzen unabhängiger Zufallsvariablen additiv verhalten.
. Diese Eigenschaft ist eine einfache Anwendung der Tatsache, dass sich die Varianzen unabhängiger Zufallsvariablen additiv verhalten.Ferner gilt für suffiziente Statistiken
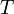 , dass die Fisher-Information bezüglich
, dass die Fisher-Information bezüglich 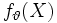 dieselbe wie für
dieselbe wie für 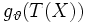 ist, wobei
ist, wobei 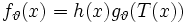 gilt.
gilt.Benutzt wird die Fisher-Information speziell in der Cramer-Rao-Ungleichung, wo sie bei Gültigkeit der angesprochenen Regularitätsbedingung eine untere Schranke für die Varianz eines Schätzers für
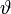 liefert.
liefert.Erweiterungen auf höhere Dimensionen
Falls das Modell von mehreren Parametern
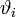 mit
mit 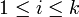 abhängt, lässt sich die Fisher-Information als symmetrische Matrix definieren, wobei
abhängt, lässt sich die Fisher-Information als symmetrische Matrix definieren, wobeigilt. Die Eigenschaften bleiben im wesentlichen erhalten.
Wikimedia Foundation.

![\mathcal{I}(\vartheta)
=
\mathrm{E}
\left[
\left(
\frac{\partial}{\partial\vartheta} \log \prod_{l=1}^{n} f_{\vartheta}(X_l)
\right)^2
\right]](/pictures/dewiki/54/6132cc39ee934eb279cef5c38a184f54.png)
![\mathrm{E}
\left[
\frac{\partial}{\partial\vartheta} \log \prod_{l=1}^{n} f_{\vartheta}(X_l)
\right]
= 0](/pictures/dewiki/99/c02877ebb0b5978b49f1911a01ba7652.png)
![\mathcal{I}_{ij}(\vartheta)
=
\mathrm{E}
\left[
\frac{\partial}{\partial\vartheta_{i}} \log \prod_{l=1}^{n} f_{\vartheta}(X_l) \frac{\partial}{\partial\vartheta_{j}} \log \prod_{l=1}^{n} f_{\vartheta}(X_l)
\right]](/pictures/dewiki/54/6b041ad5b9303cfd6a0fae6a0a76e6f0.png)