Wahrscheinlichkeitsdichte

Der Begriff der Wahrscheinlichkeitsdichtefunktion, oft kurz Wahrscheinlichkeitsdichte oder nur Dichte (abgekürzt WDF oder pdf von engl. probability density function), ist eng mit dem Begriff der stetigen Zufallsvariablen verknüpft: Die Wahrscheinlichkeitsdichte ist ein Hilfsmittel, mit dem sich die Wahrscheinlichkeit berechnen lässt, dass eine stetige Zufallsvariable zwischen zwei reellen Zahlen a und b liegt.

Einfache zufällige Prozesse lassen sich durch die konkrete Angabe von Wahrscheinlichkeitsräumen modellieren, d. h. durch Angabe einer Menge Ω von Elementarereignissen und eines Wahrscheinlichkeitsmaßes P, das Ereignissen, also Teilmengen von Ω, eine Wahrscheinlichkeit zwischen 0 und 1 zuordnet. Enthält Ω nur endlich oder höchstens abzählbar viele Elemente ω, die alle eine Wahrscheinlichkeit q(ω) besitzen, so ist das dazugehörige Wahrscheinlichkeitsmaß

$P(A)=\sum_{\omega \in A}q(\omega) \quad \forall A\subseteq \Omega\;.$

Enthält Ω überabzählbar viele Elemente, so wird die Angabe eines Wahrscheinlichkeitsmaßes auf ähnliche Weise nicht möglich sein. Man kann zeigen, dass einzelne Elementarereignisse aus Ω nun keine von Null verschiedene Wahrscheinlichkeit haben. Um dennoch praktikabel entsprechende Zufallsexperimente modellieren zu können, führt man die Begriffe der Zufallsvariablen und der Wahrscheinlichkeitsdichte ein. Eine Abbildung 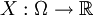$X:\Omega \rightarrow \R$ wird Zufallsvariable genannt. Eine Funktion 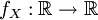$f_X:\R \rightarrow \R$ heißt nun Wahrscheinlichkeitsdichte von X, falls gilt

$P(\{\omega:a<X(\omega)<b\})=\int_a^bf_X(t)\mathrm dt.$

Für P({ω:a < X(ω) < b}) schreibt man oft kurz P{a < X < b}.

Ist die Dichtefunktion einer Zufallsvariablen bekannt, muss Ω nicht explizit angegeben werden. Der zufällige Prozess wird dann nicht mehr durch Ω und P modelliert, sondern alle interessierenden Wahrscheinlichkeiten können mit dem Integral über die Dichtefunktion berechnet werden.

Eigenschaften

Mathematisch gesehen ist die Funktion f somit eine Dichte (siehe Satz von Radon-Nikodym) der Verteilung von X bezüglich des Lebesgue-Maßes. Eine solche Dichte existiert genau dann, wenn

$P(X \in N) = 0$

für jede Borel-Nullmenge N (Satz von Radon-Nikodym).

Die Stetigkeit der Verteilungsfunktion bzw. die Eigenschaft P(X = x) = 0 für alle x ist hierfür notwendig, aber nicht hinreichend. Beispielsweise lässt sich eine Zufallsvariable konstruieren, die als Werte nur Zahlen annimmt, deren Ziffern in der Menge 1,2,3,4,5,6 liegen (etwa die Zahl 0,5364142...). Diese Zufallsvariable besitzt eine stetige Verteilungsfunktion, aber keine Dichte, da die Ziffern 7, 8, 9, 0 nicht vorkommen (vgl. Cantor-Menge).

Zusammenhang von Verteilungsfunktion und Dichtefunktion

Die Verteilungsfunktion F erhält man als Integral über die Dichtefunktion:

$F(x) = \int_{-\infty}^x f(t)\,\operatorname dt$

Umgekehrt gilt: Wenn die Verteilungsfunktion F differenzierbar ist, ist ihre Ableitung eine Dichtefunktion der zugehörigen Verteilung:

$f(x) = F^\prime(x) = \frac{\operatorname{d}F(x)}{\operatorname{d}x}$

Das gilt auch dann noch, wenn es abzählbar viele Stellen x gibt, an denen F stetig, aber nicht differenzierbar ist; welche Werte man an diesen Stellen für f(x) verwendet, ist unerheblich.

Beispiel

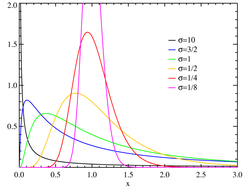
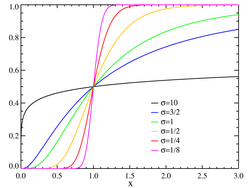Verteilungsfunktion der Lognormalverteilung (mit μ = 0)

Dichtefunktion der Lognormalverteilung
(mit μ = 0)

Verteilungsfunktion und Dichtefunktion der Lognormalverteilung (mit μ = 0)

Normierung

Die Fläche unter der Dichtefunktion muss immer den Inhalt 1 besitzen, d. h.

$\int_{-\infty}^\infty f(x) \, {\rm d}x = 1$.

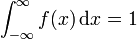Mehrdimensionale Zufallsvariable

Der Begriff der Verteilungsfunktion kann auch auf mehrdimensionale Zufallsvariablen, d.h. Zufallsvariablen, die Vektorwerte annehmen, erweitert werden: Hier ist in der Notation 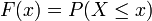$F(x)=P(X\leq x)$ das x ein Vektor und das 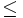$\leq\,$-Zeichen komponentenweise zu lesen. F ist also hierbei eine Abbildung von 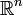$\R^n\,$ in das Intervall [0,1]. Wenn F eine differenzierbare Funktion ist, entsteht die Dichte durch partielle Differentiation:

$f:= \frac{\partial^n F(x_1,x_2, \ldots, x_n)}{\partial x_1 \cdots \partial x_n},$

dann erfüllt f die Identität

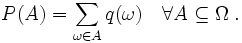
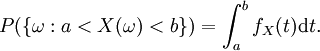
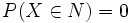
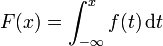
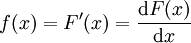
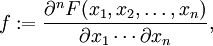
$\int_{a_1}^{b_1} \cdots \int_{a_n}^{b_n} f(x_1, \ldots, x_n)\ \mathrm{d}x_n \cdots \mathrm{d}x_1 = P(X \in [a_1,b_1] \times \cdots \times [a_n,b_n]).$