Friedmann-Robertson-Walker-Universum
- Friedmann-Robertson-Walker-Universum
-
Die Friedmann-Lemaître-Robertson-Walker (FLRW) Metrik ist eine exakte Lösung der einsteinschen Feldgleichungen der allgemeinen Relativitätstheorie und beschreibt eine homogene, isotrope Expansion des Universums bzw. Zusammenziehen des Universums. Sie ist unter unterschiedlichen Kombinationen der Namen der vier Wissenschaftler Alexander Friedmann, Georges Lemaître, Howard Percy Robertson und Arthur Geoffrey Walker bekannt, z. B. Friedmann-Robertson-Walker (FRW) oder Robertson-Walker (RW).
Die FLRW-Metrik wird als erste Näherung für das kosmologische Standard-Urknall-Modell des Universums verwendet. Da die FLRW Homogenität voraussetzt, wird oft fälschlicherweise behauptet, dass das Urknall-Modell nicht die Klumpigkeit des Universums erklären könne. Die FLRW wird tatsächlich nur als erste Näherung für die Entwicklung des Universums benutzt, weil sie so einfach zu berechnen ist. Modelle, welche die Klumpigkeit des Universums errechnen werden, erweitern die FLRW. Im Jahr 2003 schienen die theoretischen Konsequenzen der verschieden Erweiterungen zur FLRW bereits gut verstanden. Das Ziel war es, diese mit den Beobachtungen der Projekte COBE und WMAP in Einklang zu bringen.
Die Metrik kann geschrieben werden als:
![ds^2 = c^2 dt^2-a(t)^2[dr^2+\bar{r}^2 d\Omega^2]](/pictures/dewiki/52/4af6b51fd315eb8e9f276de6fb1e7ffa.png)
mit:
- a(t) = der Skalenfaktor des Universums zur Zeit t
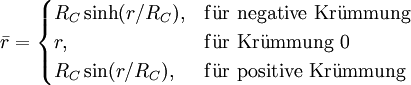
- mit
- RC = der Absolutwert des Krümmungsradius
- dΩ2 = dθ2 + sin2θdφ2
In dieser Formulierung der Metrik,
- bezeichnet r den Abstand vom mitbewegten Beobachter
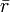 bezeichnet den kovarianten Abstand.
bezeichnet den kovarianten Abstand.
Wenn man die FLRW-Metrik sowie einen passenden Energie-Impuls-Tensor voraussetzt, reduzieren sich die einsteinschen Feldgleichungen auf die Friedmann-Gleichungen. Die Lösung der Friedmann-Gleichungen ist der zeitliche Verlauf des Skalenfaktors a(t) der FLRW-Metrik. Alle Beobachtungen im Universum auf hinreichend großen Längenskalen (nämlich größer als die größten identifizierbaren Objekte im Universum, die Galaxienhaufen) lassen sich durch ein fast-FLRW-Modell gut erklären. Ein fast-FLRW-Modell folgt der FLRW-Metrik, wobei die Entwicklung der Materieverteilung aus primordialen Fluktuationen als kleine Störung berechnet werden kann. In einem exakten FLRW-Modell gibt es keine Galaxienhaufen, Sterne oder Menschen, da diese Objekte eine höhere Dichte aufweisen als der Durchschnitt des Universums.
Trotzdem wird ein fast-FLRW-Model, der Kürze wegen, als FLRW-Modell (oder FRW-Modell) bezeichnet.
Weblinks
Literaturhinweise
- Ray d'Inverno: Introducing Einstein's Relativity. Oxford University Press, Oxford 1992, ISBN 0-19-859686-3 (Chapter 23 bietet eine knappe, klare Einführung in die FLRW-Modelle).
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Friedmann-Lemaître-Robertson-Walker-Universum — Die Friedmann Lemaître Robertson Walker (FLRW) Metrik ist eine exakte Lösung der einsteinschen Feldgleichungen der allgemeinen Relativitätstheorie und beschreibt eine homogene, isotrope Expansion des Universums bzw. Zusammenziehen des Universums … Deutsch Wikipedia
Friedmann-Robertson-Walker-Modell — Die Friedmann Lemaître Robertson Walker (FLRW) Metrik ist eine exakte Lösung der einsteinschen Feldgleichungen der allgemeinen Relativitätstheorie und beschreibt eine homogene, isotrope Expansion des Universums bzw. Zusammenziehen des Universums … Deutsch Wikipedia
Friedmann-Lemaître-Robertson-Walker-Modell — Die Friedmann Lemaître Robertson Walker (FLRW) Metrik ist eine exakte Lösung der einsteinschen Feldgleichungen der allgemeinen Relativitätstheorie und beschreibt eine homogene, isotrope Expansion des Universums bzw. Zusammenziehen des Universums … Deutsch Wikipedia
Robertson-Walker-Metrik — Die Friedmann Lemaître Robertson Walker (FLRW) Metrik ist eine exakte Lösung der einsteinschen Feldgleichungen der allgemeinen Relativitätstheorie und beschreibt eine homogene, isotrope Expansion des Universums bzw. Zusammenziehen des Universums … Deutsch Wikipedia
Friedmann-Lemaître-Robertson-Walker-Metrik — Die Friedmann Lemaître Robertson Walker (FLRW) Metrik ist eine exakte Lösung der einsteinschen Feldgleichungen der allgemeinen Relativitätstheorie und beschreibt eine homogene, isotrope Expansion des Universums bzw. Zusammenziehen des Universums … Deutsch Wikipedia
Friedmann-Gleichung — Die Friedmann Gleichungen beschreiben theoretisch die Entwicklung des Universums. Konkreter machen sie je nach Energiegehalt des Universums Voraussagen über dessen Expansion oder Kontraktion. Man erhält die Gleichungen durch Anwendung des… … Deutsch Wikipedia
Friedmann-Gleichungen — Die Friedmann Gleichungen beschreiben theoretisch die Entwicklung des Universums. Konkreter machen sie je nach Energiegehalt des Universums Voraussagen über dessen Expansion oder Kontraktion. Man erhält die Gleichungen durch Anwendung des… … Deutsch Wikipedia
Friedmann-Weltmodelle — Die Friedmann Gleichungen beschreiben theoretisch die Entwicklung des Universums. Konkreter machen sie je nach Energiegehalt des Universums Voraussagen über dessen Expansion oder Kontraktion. Man erhält die Gleichungen durch Anwendung des… … Deutsch Wikipedia
FLRW-Universum — Die Friedmann Lemaître Robertson Walker (FLRW) Metrik ist eine exakte Lösung der einsteinschen Feldgleichungen der allgemeinen Relativitätstheorie und beschreibt eine homogene, isotrope Expansion des Universums bzw. Zusammenziehen des Universums … Deutsch Wikipedia
Expandierendes Universum — Die Expansion des Universums beschreibt eine zeitliche Veränderung, nämlich eine Ausdehnung bzw. Vergrößerung, des Universums. Albert Einstein und Willem de Sitter beschrieben 1917 zum ersten Mal das Universum mit dem Formalismus der allgemeinen… … Deutsch Wikipedia
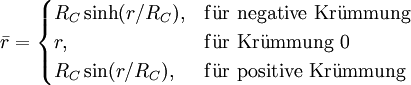
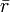 bezeichnet den kovarianten Abstand.
bezeichnet den kovarianten Abstand.
![ds^2 = c^2 dt^2-a(t)^2[dr^2+\bar{r}^2 d\Omega^2]](/pictures/dewiki/52/4af6b51fd315eb8e9f276de6fb1e7ffa.png)