Funktionenschar

Parabelschar y = a · x²
(Bündel in (0, 0) und Büschel in a)

Eine Kurvenschar (auch Funktionsschar) ist eine Menge verschiedener Kurven, deren Abbildungsvorschriften sich in mindestens einem Parameter unterscheiden. Sonderfall ist das Büschel (einparametrige Schar) und Bündel (Schar mit einem gemeinsamen Punkt).

Definition

Die Schar ist eine Menge von Punkten auf einer Kurve, Kurven auf einer Fläche oder Flächen im Raum, die jeweils durch eine Gleichung oder ein System von Gleichungen mit veränderlichen Parametern beschrieben werden.

Gemäß einer anderen Definition ergibt sich eine Kurvenschar aus dem Graphen von Funktionen, in denen ein freier Parameter der betreffenden Funktion in Parameterdarstellung variiert wird.

Zur Veranschaulichung von Funktionsscharen eignen sich besonders Dynamische Geometrie-Systeme.

Sonderfälle

• Handelt es sich bei allen Schaubildern der Funktionsschar um Geraden, so spricht man von einer Geradenschar.
  • Verlaufen dabei die einzelnen Geraden auch noch parallel, so bezeichnet man sie als Parallelenschar.
  • Wenn sich alle beteiligten Geraden in einem Punkt schneiden, handelt es sich um ein Geradenbündel.
  • Wenn sich alle beteiligten Geraden sowohl in einem Punkt schneiden als auch in einer Ebene liegen, handelt es sich um ein Geradenbüschel.

• Handelt es sich bei allen Kurven der Schar um Parabeln, so spricht man von einer Parabelschar.

Beispiele

• alle Kurven der zur Funktion y = p gehörigen Kurvenschar verlaufen parallel zur x-Achse. Der Parameter dieser Kurvenschar ist p.
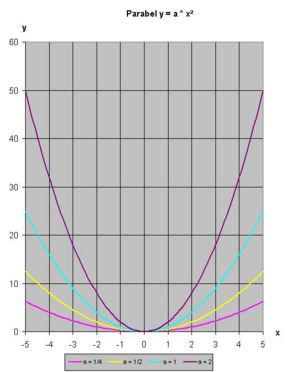
• alle Kurven der zur Funktion y_a = ax² gehörigen Schar sind Parabeln durch den Koordinatenursprung (siehe Abbildung). Der Parameter ist a.
• alle Kurven der zur Relation x² + y² = r² gehörigen Schar sind konzentrische Kreise. Der Parameter ist r.