Diskrete Gleichverteilung

Wahrscheinlichkeitsfunktion der diskreten Gleichverteilung auf $\{0,1,\dots,20\}$, d.h. n = 21

Die diskrete Gleichverteilung ist eine statistische Wahrscheinlichkeitsverteilung (Gleichverteilung). Eine diskrete Zufallsvariable X mit endlich vielen Ausprägungen hat eine diskrete Gleichverteilung, wenn die Wahrscheinlichkeit für jede ihrer Ausprägungen $x_i (i=1, \dots , n)$ gleich ist.

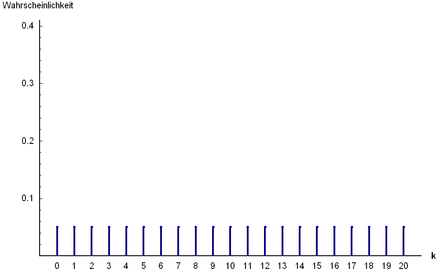
Wahrscheinlichkeitsfunktion

Die Wahrscheinlichkeitsfunktion der diskreten Gleichverteilung ist:

$\operatorname{P}(X = x) =f(x)= \begin{cases} \frac {1}{n} & \mathrm{f\ddot ur}\; x = x_i (i = 1, \dots , n) \\ 0 & \mbox{sonst} \end{cases}$

und damit genügt sie der Verteilungsfunktion

$F_X(t)= P(X\leq t) = \frac{|\{k:x_k\leq t\}|}{n}$.

Im Fall x_k = k ergibt das

$F_X(t)= P(X\leq t) = \left\{\begin{matrix} 0 & \mbox{falls } & t<1 \\ \frac{\lfloor t \rfloor}{n} & \mbox{falls } & 1 \leq t < n \\ 1 & \mbox{falls } & t \geq n \end{matrix}\right.$

Der Erwartungswert ist:

$\operatorname{E}(X) = \frac{1}{n} \sum_{i=1}^n x_i$

Im Fall x_k = k besitzt die diskrete Gleichverteilung den Erwartungswert (nach der Gaußschen Summenformel)

$\operatorname{E}(X) = \frac{1}{n} \sum_{i=1}^n x_i =\frac{n+1}{2}$

und die Varianz

$\operatorname{Var}(X) = \frac {1}{n} \left(\sum_{i=1}^n x_i^2 - \frac {1}{n} \left(\sum_{i=1}^n x_i\right)^2\right) =\frac{n^2-1}{12}$.

Typischerweise findet diese Wahrscheinlichkeitsverteilung Anwendung bei Zufallsexperimenten, deren Ergebnisse gleichhäufig sind. Wenn man (mit oder ohne Begründung) annimmt, dass die n Elementarereignisse gleichwahrscheinlich sind, spricht man von einem Laplace-Experiment. Gängige Beispiele für Laplace-Experimente sind der Laplace-Würfel und die Laplace-Münze. Siehe auch Stetige Gleichverteilung, Laplace-Formel.

Beispiel

Sechsseitiger Laplace-Würfel

Das Zufallsexperiment ist: Ein Würfel wird einmal geworfen. Die möglichen Ausprägungen der Zufallsvariablen X sind: $x_1=1, x_2=2, \dots, x_6=6$. Nach der klassischen Wahrscheinlichkeitsauffassung ist die Wahrscheinlichkeit für jede Ausprägung gleich. Sie hat dann die Wahrscheinlichkeitsfunktion

$P(X = x) = f(x) = \begin{cases} \frac{1}{6} & \mathrm{f\ddot ur}\; x = x_i (i = 1, \dots , 6) \\ 0 & \mbox{sonst} \end{cases}$

mit dem Erwartungswert $\operatorname{E}(X)$ für x_i = i und n = 6:

E(X) = 7 / 2 = 3,5

und der Varianz

$V(X) = \frac {35}{12} \approx 2,92$.

Entscheidungsproblem des Marketing

Eine Anwendung in der Praxis könnte etwa ein Problem des Operations Research (Marketing) sein. Eine Unternehmung möchte ein neues Produkt auf dem Markt einführen

Man versucht, den Erfolg des Produkt quantitativ vorauszuschätzen. Es wird vereinfachend von 5 verschiedenen verkauften Stückzahlen ausgegangen: 0, 1.000, 5.000, 10.000 und 50.000. Da über die Wahrscheinlichkeit der einzelnen Absatzzahlen keine verläßliche Schätzung möglich ist, verwendet man der Einfachheit halber gleiche Wahrscheinlichkeiten.

Man kann nun den Entscheidungsprozess, d.h. die individuelle Kaufentscheidung objektivieren, also den erwarteten durchschnittlichen Absatz ermitteln und sich überlegen, etwa anhand von Entscheidungsbäumen, inwieweit erhöhte Werbeausgaben die Absatzzahlen erhöhen könnten.

Abgrenzung

Die diskrete Gleichverteilung wird oft auch nach Pierre-Simon Laplace benannt (Laplace-Würfel). Sie hat jedoch nichts mit der stetigen Laplace-Verteilung zu tun.

Weblinks

• Universität Konstanz – Interaktive Animation

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | kategorial | hypergeometrisch | Rademacher | Zipf | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | negativ binomial | erweitert negativ binomial | Compound-Poisson | diskret uniform | discrete-Phase-Type | Gauss-Kuzmin | geometrisch | logarithmisch | parabolisch-fraktal | Poisson | Poisson-Gamma | Skellam | Yule-Simon | Zeta