Galilei-Gruppe

Die Koordinatentransformation von einem Bezugssystem B₁ in ein anderes Bezugssystem B₂ nennt man Galilei-Transformation, wenn sich B₂ von B₁ nur durch eine Parallelverschiebung, eine Drehung oder eine gleichförmig geradlinige Bewegung unterscheidet.

Bemerkungen

Newton-Mechanik

B₂ ist in Bezug zu B₁ unbeschleunigt. Ist B₁ ein Inertialsystem, also ein Bezugssystem in dem nur physikalische (also newtonsche) Kräfte auftreten, so ist B₂ ebenfalls ein Inertialsystem. Ist B₁ kein Inertialsystem, also eines mit mathematischen (also scheinbaren) Kräften, so gilt dies ebenfalls für B₂. Die Newtonsche Mechanik ist Invariant bei Galilei-Transformationen.

Andere Transformationen

Eine Rotation ist keine Galilei-Transformation, da B₂ in Bezug zu B₁ beschleunigt ist. Die Transformation von kartesischen Koordinaten in Kugelkoordinaten oder eine Skalierung oder Scherung ist ebenfalls keine Galilei-Transformation.

Die Transformationen im Einzelnen

Die drei Galilei-Transformationen Verschieben (mit dem konstanten Verschiebungsvektor 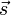$\vec s$), Verdrehen (mit der konstanten Drehmatrix D) und unbeschleunigt Bewegen (mit der konstanten Geschwindigkeit 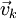$\vec v_k$) können formal zu einer einzigen Galilei-Transformation GT zusammengefasst werden: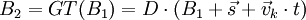

$B_2 = GT(B_1) = D \cdot (B_1 + \vec s + \vec v_k \cdot t)$

Parallelverschiebung

Ist B₂ in Bezug zu B₁ um den Verschiebungsvektor 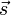$\vec s$ versch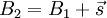oben

$B_2 = B_1 + \vec s$

lautet die entsprechende Koordinatentransformation

$\vec r(t)_2 = \vec r(t)_1 - \vec s$

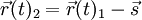
In Bezug zu B₁ scheinen die Orte verschoben, aber die Geschwindigkeit ist unverändert und folglich ebenfalls die Beschleunigung: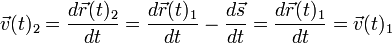

$\vec v(t)_2 = \frac {d \vec r(t)_2}{dt} = \frac {d \vec r(t)_1}{dt} - \frac {d \vec s}{dt} = \frac {d \vec r(t)_1}{dt} = \vec v(t)_1$

Drehung

Ist B₂ in Bezug zu B₁ gedreht worden (D ist eine Drehmatrix)

$B_2=D \cdot B_1$

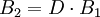
lautet die entsprechende Koordinatentransformation

$\vec r(t)_2 = D^{-1} \cdot \vec r(t)_1$

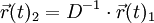
In Bezug zu B₁ sind die Orte, Geschwindigkeiten und Beschleunigungen nur gedreht. An der Physik mit ihren Kräften ändert sich nichts.

Geradlinig gleichförmige Bewegung

Hat B₂ in Bezug zu B₁ eine konstante Geschwindigkeit $\vec v_k$

$B_2 = B_1 + \vec v_k \cdot t$

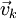
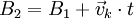
lautet die entsprechende Koordinatentransformation

$\vec r(t)_2 = \vec r(t)_1 - \vec v_k \cdot t$

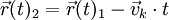
In Bezug zu B₁ wird die Geschwindigkeit verändert, aber die Beschleunigung nicht: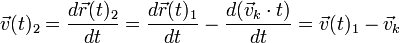

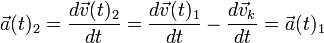
$\vec v(t)_2 = \frac {d \vec r(t)_2}{dt} = \frac {d \vec r(t)_1}{dt} - \frac {d (\vec v_k \cdot t)}{dt} = \vec v(t)_1 - \vec v_k$

$\vec a(t)_2 = \frac {d \vec v(t)_2}{dt} = \frac {d \vec v(t)_1}{dt} - \frac {d \vec v_k}{dt} = \vec a(t)_1$

In der Maxwellschen Elektrodynamik führt diese Galilei-Transformation zu Problemen und ist durch die Lorentz-Transformation ersetzt worden.