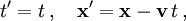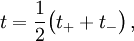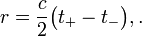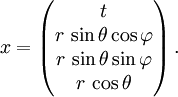Absolutsystem

In der Physik ist ein Inertialsystem (von lateinisch iners „untätig, träge“) ein Koordinatensystem in dem sich kräftefreie Körper geradlinig, gleichförmig bewegen. In einem Inertialsystem gilt also das Newtonsche Trägheitsgesetz in seiner einfachsten Form, nach der kräftefreie Körper ihre Geschwindigkeit in Betrag und Richtung beibehalten und Beschleunigungen proportional zur anliegenden Kraft erfolgen. Der Begriff Inertialsystem wurde erstmals von Ludwig Lange (1885) verwendet.

Bemerkenswerterweise drehen sich Inertialsysteme (innerhalb der derzeitigen Messgenauigkeit) nicht gegenüber dem Fixsternhimmel und sind gegenüber den Fixsternen gradlinig gleichförmig bewegt.

Verschiedene Inertialsysteme bewegen sich gegeneinander geradlinig und gleichförmig. Demgegenüber drehende oder anderweitig beschleunigte Bezugssysteme sind keine Inertialsysteme.

Ein mit der Erde mitrotierendes Bezugssystem ist nicht inertial. In ihm gibt es keine kräftefreien Teilchen, sondern es treten Scheinkräfte auf.

Newtons Mechanik

In Newtons Mechanik hängen zwei Inertialsysteme durch eine Galilei-Transformation zusammen.

Galilei-Transformationen bilden eine Gruppe. Zu ihr gehört die zeitliche oder räumliche Verschiebung, die den zeitlichen und räumlichen Ursprung des einen Systems auf denjenigen des anderes Systems abbildet. Da ein Inertialsystem bei einer räumlichen oder zeitlichen Verschiebung in ein Inertialsystem übergeht, zeichnen Inertialsysteme keinen Ort und keinen Zeitpunkt aus. Der Raum und die Zeit sind homogen.

Zur Galilei-Gruppe gehört die Drehung, die die zeitlich unveränderlichen Bezugsrichtungen (oben, vorn, rechts) des einen Systems auf die ebenso zeitlich unveränderlichen Richtungen des anderen Systems abbildet. Da ein Inertialsystem bei einer Drehung in ein Inertialsystem übergeht, zeichnen Inertialsysteme keine Richtung aus. Der Raum ist isotrop.

Zur Galilei-Gruppe gehört die Transformation,

$t^\prime=t\,,\quad \mathbf x^\prime = \mathbf x - \mathbf v\,t\,,$

mit der gegeneinander mit gleichbleibender Geschwindigkeit 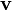$\mathbf v$ bewegte Beobachter Zeiten und Ortsbezeichnungen ineinander umrechnen.

Da die Gesetze der newtonschen Mechanik in allen Inertialsystemen gelten, die sich relativ zueinander mit konstanter Geschwindigkeit bewegen, gibt es kein bevorzugtes Bezugssystem und keine Möglichkeit, eine Geschwindigkeit absolut zu messen. Dies ist das Relativitätsprinzip der newtonschen Mechanik.

Spezielle Relativitätstheorie

Statt der Galilei-Transformation zwischen Inertialsystemen der Newtonschen Physik vermitteln in der relativistischen Physik Lorentz-Transformationen und raum-zeitliche Verschiebungen, wie die Koordinaten zusammenhängen, mit denen gleichförmig bewegte Beobachter bezeichnen, wann und wo Ereignisse stattfinden. Zusammen mit den räumlichen und zeitlichen Verschiebungen bilden Lorentztransformationen die Poincaré-Gruppe.

Nach folgendem idealisierten Verfahren ordnet ein gleichförmig bewegter Beobachter wie beim Radar jedem Ereignis seine inertialen Koordinaten zu: Er sendet einen Lichtstrahl zum Ereignis und misst mit seiner Uhr die Startzeit t ₋ und die Zeit t ₊ , zu der der in Ereignis reflektierte Lichtstrahl wieder bei ihm eintrifft. Als Zeit, zu der das Ereignis stattgefunden hat, verwendet er den Mittelwert

$t=\frac{1}{2}\bigl(t_++t_-\bigr)\,,$

als Entfernung die Hälfte der Laufzeit des hin und her laufenden Lichtes mal der Lichtgeschwindigkeit c

$r=\frac{c}{2}\bigl(t_+-t_-\bigr),.$

Darüber hinaus bestimmt er Winkel θ und $\varphi$ zwischen Bezugsrichtungen, die er gewählt hat, und dem auslaufenden Lichtstrahl. Damit ordnet er dem Ereignis folgende Koordinaten zu:

$x= \begin{pmatrix} t\\ r\,\sin\theta\cos\varphi\\ r\,\sin\theta\sin\varphi\\ r\,\cos\theta \end{pmatrix}\,.$

Der reflektierte Lichtstrahl kommt nur dann für jedes Ereignis aus der Richtung des auslaufenden Lichtstrahls zurück, wenn sich der Beobachter nicht dreht. Auf diese Art kann der Beobachter unterscheiden, ob er sich dreht oder ob er von anderen Objekten umkreist wird.

Allgemeine Relativitätstheorie

Die Allgemeine Relativitätstheorie ist so formuliert, dass ihre Gleichungen in jedem Koordinatensystem gelten. Die Weltlinien frei fallender Teilchen sind die Geraden (genauer Geodäten) der gekrümmten Raumzeit. Gravitation zeigt sich im freien Fall an der Gezeitenwirkung, dass benachbarte Geodäten aufeinander zu oder voneinander weg streben und sich wiederholt schneiden können. Umkreisen beispielsweise zwei Raumstationen mit gleichem Abstand in verschiedenen Ebenen die Erde, so schneiden sich ihre Bahnkurven und Weltlinien dort, wo sich die Bahnebenen schneiden, danach nimmt ihr Abstand zu, bis sie einen Viertelkreis durchlaufen haben, dann wieder ab, bis sich ihre Bahn nach einem Halbkreis wieder kreuzt. Diese Auswirkung ungleichmäßiger Gravitation (sie wirkt an verschiedenen Orten in verschiedene Richtung oder mit verschiedener Stärke) heißt Gezeitenwirkung. Sie nimmt bei kleinen Abständen mit dem Abstand zu. Kann man die Gezeitenwirkung vernachlässigen, so gilt im freien Fall die Spezielle Relativitätstheorie.

Der Begriff des mitfallenden Bezugssystems ersetzt in der Allgemeinen Relativitätstheorie den Begriff des Inertialsystems.