Gangunterschied

Gangunterschied Δs am Beispiel eines Doppelspalts (in der Graphik ist Δs = λ)

Der Gangunterschied ist die Wegdifferenz (Wegunterschied) zweier oder mehrerer kohärenter Wellen. Die Wegdifferenz Δs = s₂ − s₁ ist entscheidend für das Auftreten von Interferenzerscheinungen.

Bedingungen für konstruktive bzw. destruktive Interferenz zweier Wellen

Beträgt der Gangunterschied zweier Wellen gleicher Wellenlänge und Amplitude genau eine halbe Wellenlänge (plus einem beliebigen ganzzahligen Vielfachen der Wellenlänge), so löschen sich die beiden Teilwellen aus. Man nennt diese Intensitätsschwächung destruktive Interferenz:

$\Delta s = (k + 0{,}5) \lambda \quad \text{mit} \quad k = 0, \pm 1, \pm 2, \pm 3, \dots, \pm n$

Beträgt er ein ganzzahliges Vielfaches der Wellenlänge, addieren sich die Amplituden der beiden Teilwellen. In diesem Fall liegt konstruktive Interferenz vor:

$\Delta s = k \lambda \quad \text{mit} \quad k = 0, \pm 1, \pm 2, \pm 3, \dots, \pm n$

Bei Werten dazwischen ergibt sich eine teilweise Auslöschung.

Bestimmung des Gangunterschieds bei elektromagnetischen Wellen

Bei elektromagnetischen Wellen hat man es typischerweise mit der Situation zu tun, dass die absolute Weglänge den Gangunterschied um mehrere Größenordnungen übersteigt (konkret ca. ein halber Meter zu ca. einem halben Mikrometer, also sechs Zehnerpotenzen). Daher können geometrische Konstruktionen hier immer mit parallelen Strahlenbündeln vorgenommen werden (im Gegensatz beispielsweise zur Situation bei Wasserwellen). Mit Hilfe rechtwinkliger Dreiecke an Stellen, wo Beugung an einem Gegenstand auftritt, kann man den Beugungswinkel bzw. den Beobachtungswinkel mit dem Gangunterschied und der charakteristischen Länge (bzw. Breite) des beugenden Gegenstands in Beziehung bringen.

Beispiel Beugung am Einzelspalt, Beobachtungswinkel θ.
Die roten Pfeile verdeutlichen den Gangunterschied einzelner Strahlen gegenüber dem oberen Strahl.
Die blaue Sinuskurve illustriert die Feldstärke der einzelnen Strahlen entlang der schwarzen Linie zu einem beispielhaft gewählten Zeitpunkt. Destruktive Interferenz besteht für die Richtungen, für die sich hier ganze Perioden ergeben.

Beispiel Bragg-Reflexion

Bragg-Reflexion

Bei der Bragg-Reflexion ist der Gangunterschied zwischen den Strahlen zweier benachbarter Gitterebenen gerade Δs = 2δ. Konstruktive Interferenz zwischen zwei Strahlen ergibt sich für $\Delta s = n \cdot \lambda$, woraus die Bragg-Bedingung $n \cdot \lambda = 2 d\cdot \sin \theta$ folgt.

Beugung am Einzelspalt

Betrachtet man am Einzelspalt die in Richtung θ auslaufenden Strahlen, so haben diese gegeneinander einen Gangunterschied. Das Interferenzmuster ergibt sich dadurch, dass sich die einzelnen Strahlen in Richtung θ in einem entfernten Punkt (der Wand) überlagern. Beträgt der Gangunterschied zwischen dem Strahl am oberen Ende und dem am unteren Ende des Spalts D, so kommt es immer dann zu einer Auslöschung der in dieser Richtung gemessenen Gesamtintensität, wenn D ein von null verschiedenes ganzzahliges Vielfaches der Wellenlänge ist, da sich dann die positiven und die negativen Feldstärken der dazwischenliegenden Strahlen jeweils aufheben. Für alle anderen Richtungen verbleibt eine Restintensität. In der Richtung „geradeaus“ (k=0) tritt ein besonders helles Intensitätsmaximum auf, da dort alle Strahlen gleichphasig sind und daher konstruktiv interferieren.^[1]

Da es sich hier um eine Schar von Strahlen handelt, die alle einen Gangunterschied $\Delta s \in [0,D]$ gegenüber dem oberen Strahl haben, weicht die Bedingung für die destruktive Interferenz $\ D = k \lambda \ (k\neq 0)$ von den eingangs erwähnten Werten ab, bei denen es um Auslöschung bei zwei Wellen ging. Der Gangunterschied zwischen den beiden Rändern hängt mit der Spaltbreite b und dem Richtungswinkel θ wie folgt zusammen: $\ D = \sin \theta \cdot b$. Daraus ergeben sich Minima für die Richtungen θ, für die

$\sin \theta = \frac{k \lambda}{b} \quad \text{mit} \quad k\neq 0$ gilt.

Zusammenhang mit der Phasendifferenz

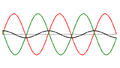
Einem Gangunterschied Δs entspricht eine Phasenverschiebung $\Delta\varphi = \frac{\Delta s}{\lambda} \cdot 2\pi$ im Bogenmaß und $\Delta\varphi = \frac{\Delta s}{\lambda} \cdot 360^\circ$ im Gradmaß. Die Phasendifferenz zweier Wellen ist für die Verstärkung und Auslöschung verantwortlich.

• Überlagerung zweier sinusförmiger Wellen bei der Phasenverschiebung von:
• 

  … 20°

• 

  … 170°

• 

  … 180°

Der Verlauf der beiden Einzelwellen ist rot und grün dargestellt, ihre Summe wird durch die schwarze Linie angegeben. Die Phasendifferenz von 180° entspricht der Wegdifferenz einer halben Wellenlänge (ggf. zuzüglich ganzzahligen Vielfachen der Wellenlänge), was erkennbar dazu führt, dass keine Amplitude gemessen wird, also ein Beugungsminimum vorliegt.

Einzelnachweise

1. ↑ Für ein Bild des Interferenzmusters siehe Gerthsen, Abschnitt Spalt- und Lochblende im Kapitel Wellenoptik, ISBN 3-540-16155-4

Weblinks

• Berechnung des Gangunterschiedes bei der Zwei-Quellen-Interferenz (LEIFI-Physik)