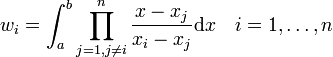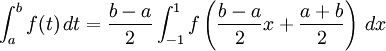Gaußquadratur

Die Gauß-Quadratur (nach Carl Friedrich Gauß) ist ein Verfahren zur numerischen Berechnung von Integralen, das bei gegebenen Freiheitsgraden eine optimale Approximation des Integrals liefert. Bei diesem Verfahren wird die zu integrierende Funktion g aufgeteilt in 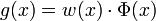$g(x) = w(x) \cdot \Phi(x)$, wobei w eine Gewichtsfunktion ist und Φ durch ein spezielles Polynom mit speziell gewählten Auswertungspunkten x_i approximiert wird. Dieses Polynom lässt sich exakt integrieren. Das Verfahren ist also von der Form

$\int_{a}^{b}g(x)\,\mathrm dx = \int_{a}^{b}\Phi(x)w(x)\,\mathrm dx \approx \int_{a}^{b}p_n(x)w(x)\,\mathrm dx = \sum_{i=1}^{n}\Phi(x_{i})w_{i}$.

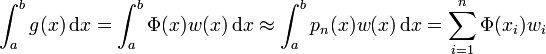Für die Gewichtsfunktion w gilt, sie ist größer gleich Null, hat endlich viele Nullstellen und ist integrierbar, Φ ist eine stetige Funktion. Der Integrationsbereich [a,b] ist nicht auf endliche Intervalle beschränkt. Weiterhin werden x_i als Knoten oder Abszissenwerte und die Größen w_i als Gewichte bezeichnet.

Eigenschaften

Um optimale Genauigkeit zu erreichen, müssen die Abszissenwerte x_i einer Gauß-Quadraturformel vom Grad n genau den Nullstellen des n-ten orthogonalen Polynoms P_n vom Grad n entsprechen. Die Polynome P₁, P₂, ..., P_n müssen dabei orthogonal bezüglich des mit w(x) gewichteten Skalarprodukts sein,

$\delta_{i,j}=\langle P_{i},P_{j}\rangle_w:=\int_{a}^{b}P_{i}(x)P_{j}(x)w(x)\,\mathrm dx$

Für die Gewichte gilt:

$w_i = \int_{a}^{b} \prod_{j=1,j\not = i}^n\frac{x-x_j}{x_i-x_j}\mathrm dx \quad i=1,\ldots,n$

Die Gauß-Quadratur stimmt für polynomiale Funktionen Φ(x), deren Grad maximal 2n − 1 ist, mit dem Wert des Integrals exakt überein. Es lässt sich zeigen, dass keine Quadraturformel existiert, die alle Polynome vom Grad 2n exakt integriert. In dieser Hinsicht ist die Ordnung des Quadraturverfahrens optimal.

Anwendung

Die gaußsche Quadratur findet Anwendung bei der numerischen Integration. Dabei werden für eine gegebene Gewichtsfunktion und einen gegebenen Grad n, der die Genauigkeit der numerischen Integration bestimmt, einmalig die Stützpunkte x_i und Gewichtswerte w_i berechnet und tabelliert. Anschließend kann für beliebige Φ(x) die numerische Integration durch einfaches Aufsummieren von gewichteten Funktionswerten erfolgen.

Dieses Verfahren ist damit potentiell vorteilhaft

1. wenn viele Integrationen mit derselben Gewichtsfunktion durchgeführt werden müssen und
2. wenn Φ(x) hinreichend gut durch ein Polynom approximierbar ist.

Für einige spezielle Gewichtsfunktionen sind die Werte für die Stützstellen und Gewichte fertig tabelliert.

Gauß-Legendre-Integration

Hier handelt es sich um die bekannteste Form der Gauß-Integration auf dem Intervall [ − 1,1], sie wird oft auch einfach als Gauß-Integration bezeichnet. Es gilt w(x) = 1. Die resultierenden orthogonalen Polynome sind die Legendre-Polynome erster Art. Die Erweiterung auf beliebige Intervalle [a,b] erfolgt durch eine Variablentransformation.

Die Stützpunkte (auch Gaußpunkte genannt) und Gewichte der Gauß-Legendre-Integration sind:

N=1	xi	wi
1	0	2
N=2	xi	wi
1	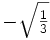$-\sqrt{\tfrac{1}{3}}$≈ -0.57735026919	1
2	$\sqrt{\tfrac{1}{3}}$ ≈ 0.57735026919	1
N=3	xi	wi
1	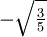$-\sqrt{\tfrac{3}{5}}$ ≈ -0.774596669241	$\tfrac{5}{9}$ ≈ 0.555555555556
2	0	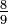$\tfrac{8}{9}$ ≈ 0.888888888889
3	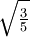$\sqrt{\tfrac{3}{5}}$ ≈ 0.774596669241	$\tfrac{5}{9}$ ≈ 0.555555555556
N=4	xi	wi
1	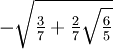$-\sqrt{ \tfrac{3}{7} + \tfrac{2}{7}\sqrt{\tfrac{6}{5}} }$ ≈ -0.861136311594053	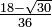$\tfrac{18-\sqrt{30}}{36}$ ≈ 0.347854845137454
2	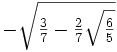$-\sqrt{ \tfrac{3}{7} - \tfrac{2}{7}\sqrt{\tfrac{6}{5}} }$ ≈ -0.339981043584856	$\tfrac{18+\sqrt{30}}{36}$ ≈ 0.652145154862546
3	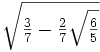$\sqrt{ \tfrac{3}{7} - \tfrac{2}{7}\sqrt{\tfrac{6}{5}} }$ ≈ 0.339981043584856	$\tfrac{18+\sqrt{30}}{36}$ ≈ 0.652145154862546
4	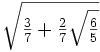$\sqrt{ \tfrac{3}{7} + \tfrac{2}{7}\sqrt{\tfrac{6}{5}} }$ ≈ 0.861136311594053	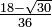$\tfrac{18-\sqrt{30}}{36}$ ≈ 0.347854845137454
N=5	xi	wi
1	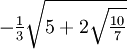$-\tfrac13\sqrt{5+2\sqrt{\tfrac{10}{7}}}$ ≈ -0.906179845938664	$\tfrac{322-13\sqrt{70}}{900}$ ≈ 0.236926885056189
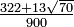2	$-\tfrac13\sqrt{5-2\sqrt{\tfrac{10}{7}}}$ ≈ -0.538469310105683	$\tfrac{322+13\sqrt{70}}{900}$ ≈ 0.478628670499366
3	0	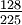$\tfrac{128}{225}$ ≈ 0.568888888888889
4	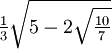$\tfrac13\sqrt{5-2\sqrt{\tfrac{10}{7}}}$ ≈ 0.538469310105683	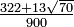$\tfrac{322+13\sqrt{70}}{900}$ ≈ 0.478628670499366
5	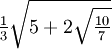$\tfrac13\sqrt{5+2\sqrt{\tfrac{10}{7}}}$ ≈ 0.906179845938664	$\tfrac{322-13\sqrt{70}}{900}$ ≈ 0.236926885056189

Gauß-Tschebyschow-Integration

Eine Variante der Gauß-Integration auf dem Intervall [ − 1,1]. Es gilt $w(x)=1/\sqrt{1-x^2}$. Die resultierenden orthogonalen Polynome sind die Tschebyschow-Polynome. Die Stützpunkte liegen hier oftmals günstiger im Vergleich zur Gauß-Legendre-Integration. Die Erweiterung auf beliebige Intervalle [a,b] erfolgt durch eine Variablentransformation. 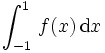Liegt der Integrand in der Form $\int_{-1}^{1}\,f(x)\,\mathrm dx$ vor, so kann er umgeformt werden in 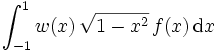$\int_{-1}^{1}w(x)\,\sqrt{1-x^2}\,f(x)\,\mathrm dx$. Zur numerischen Berechnung wird das Integral nun durch die Summe 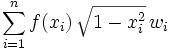$\sum_{i=1}^{n}f(x_{i})\,\sqrt{1-x_{i}^2}\,w_{i}$ approximiert.

Gauß-Hermite-Integration

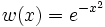Gauß-Integration auf dem Intervall $(-\infty,\infty)$. Es gilt $w(x)=e^{-x^2}$. Die resultierenden orthogonalen Polynome sind die Hermite-Polynome. Liegt der Integrand in der Form 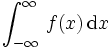$\int_{-\infty}^{\infty}\,f(x)\,\mathrm dx$ vor, so kann er umgeformt werden in 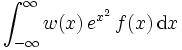$\int_{-\infty}^{\infty}w(x)\,e^{x^2}\,f(x)\,\mathrm dx$. Zur numerischen Berechnung wird das Integral nun durch die Summe 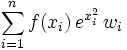$\sum_{i=1}^{n}f(x_{i})\,e^{x_{i}^2}\,w_{i}$ approximiert.

Stützpunkte und Gewichte der Gauß-Hermite-Integration:

N=2	xi	wi	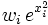$w_i\,e^{x_i^2}$
1	-0.707106781187	0.886226925453	1.46114118266
2	0.707106781187	0.886226925453	1.46114118266
N=3	xi	wi	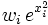$w_i\,e^{x_i^2}$
1	-1.22474487139	0.295408975151	1.32393117521
2	0	1.1816359006	1.1816359006
3	1.22474487139	0.295408975151	1.32393117521
N=4	xi	wi	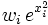$w_i\,e^{x_i^2}$
1	-1.65068012389	0.0813128354472	1.2402258177
2	-0.524647623275	0.804914090006	1.05996448289
3	0.524647623275	0.804914090006	1.05996448289
4	1.65068012389	0.0813128354472	1.2402258177

Gauß-Laguerre-Integration

Gauß-Integration auf dem Intervall 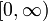$[0,\infty)$. Es gilt w(x) = e ^{− x}. Die resultierenden orthogonalen Polynome sind die Laguerre-Polynome. Liegt der Integrand in der Form 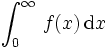$\int_{0}^{\infty}\,f(x)\,\mathrm dx$ vor, so kann er umgeformt werden in 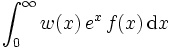$\int_{0}^{\infty}w(x)\,e^{x}\,f(x)\,\mathrm dx$. Zur numerischen Berechnung wird das Integral nun durch die Summe $\sum_{i=1}^{n}f(x_{i})\,e^{x_i}\,w_{i}$ approximiert.

Stützpunkte und Gewichte der Gauß-Laguerre-Integration:

N=2	xi	wi	$w_i\,e^{x_i}$
1	0.585786437627	0.853553390593	1.53332603312
2	3.41421356237	0.146446609407	4.45095733505
N=3	xi	wi	$w_i\,e^{x_i}$
1	0.415774556783	0.711093009929	1.07769285927
2	2.29428036028	0.278517733569	2.7621429619
3	6.28994508294	0.0103892565016	5.60109462543
N=4	xi	wi	$w_i\,e^{x_i}$
1	0.322547689619	0.603154104342	0.832739123838
2	1.74576110116	0.357418692438	2.04810243845
3	4.53662029692	0.038887908515	3.63114630582
4	9.3950709123	0.000539294705561	6.48714508441

Variablentransformation bei der Gauß-Quadratur

Ein Integral über [a, b] wird auf ein Integral über [−1, 1] zurückgeführt, bevor man die Methode der Gauß-Quadratur anwendet. Dieser Übergang kann auf folgende Weise geschehen:

$\int_a^b f(t)\,dt = \frac{b-a}{2} \int_{-1}^1 f\left(\frac{b-a}{2}x + \frac{a+b}{2}\right)\,dx$

Nach Anwendung der Gauß-Quadratur gilt die Approximation

$\int_a^b f(t)\,dt \approx \frac{b-a}{2} \sum_{i=1}^n w_i f\left(\frac{b-a}{2}x_i + \frac{a+b}{2}\right)$.

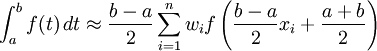Weblinks

• Mathepedia: Tabelle mit Gewichten
• efunda: Abscissas and Weights of Gauss-Laguerre Integration

Literatur

• Krylov, V. I.: "Approximate Calculation of Integrals". MacMillan, New York, 1962.
• Davis, P. und Rabinowitz, P.: Methods of Numerical Integration. 2nd. ed., Academic Press, 1984.
• Stroud, A. H. und Secrest, D.: Gaussian Quadrature Formulas. Prentice-Hall, Englewood Cliffs, NJ, 1966.
• Stroud, A. H.: Approximate Calculation of Multiple Integrals. Prentice-Hall, Englewood Cliffs, NJ, 1971.