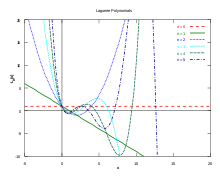
Laguerre-Polynome

Die ersten sechs Laguerre-Polynome

Laguerre-Polynome (benannt nach Edmond Laguerre) sind die Lösungen der laguerreschen Differentialgleichung

$x \, y''(x) + (1-x)\,y'(x) + n y(x) = 0 \qquad n = 0,1,\ldots$

Das n-te Laguerre-Polynom lässt sich über die Rodrigues-Formel

$L_n(x):=\frac{\mathrm{e}^x}{n!} \frac{{\rm d}^n}{{\rm d}x^n}(x^n \mathrm{e}^{-x})$

darstellen. Es handelt sich dabei um ein Polynom vom Grad n. Über die ersten Laguerre-Polynome

$\,L_0(x) = 1$

$\,L_1(x) = -x+1$

$\,L_2(x) = \frac{1}{2}\,(x^2 - 4\,x + 2)$

$\,L_3(x) = \frac{1}{6}\,(-x^3 + 9\,x^2 -18\,x + 6)$

lassen sich die Weiteren über folgende Rekursionsformeln berechnen:

$(n+1) \, L_{n+1}(x) = (2\,n+1-x)\,L_n(x) - n\,L_{n-1}(x)$

$x\,L_n'(x) = n\,L_n(x) - n\,L_{n-1}(x)$

Zugeordnete Laguerre-Polynome

Die zugeordneten Laguerre-Polynome hängen mit den gewöhnlichen Laguerre-Polynomen über

$L_n^k(x) = (-1)^k \, \frac{{\rm d}^k}{{\rm d}x^k} \, L_{n+k}(x)$

zusammen. Ihre Rodrigues-Formel lautet

$L_n^k(x) = \frac{\mathrm{e}^x \, x^{-k}}{n!} \, \frac{{\rm d}^n}{{\rm d}x^n} \, (\mathrm{e}^{-x}\,x^{n+k}).$

Die zugeordneten Laguerre-Polynome erfüllen die zugeordnete Laguerre-Gleichung

$x\,y''(x) + (k+1-x)\,y'(x) + n\,y(x) = 0, \qquad n = 0,1,\ldots, \qquad k \le n.$

Die ersten zugeordneten Laguerre-Polynome lauten

$L_0^k(x) = 1$

$L_1^k(x) = -x + k + 1$

$L_2^k(x) = \frac{1}{2}\,\left[x^2 - 2\,(k+2)\,x + (k+1)(k+2)\right]$

$L_3^k(x) = \frac{1}{6}\,\left[-x^3 +3\,(k+3)\,x^2 - 3\,(k+2)\,(k+3)\,x + (k+1)\,(k+2)\,(k+3)\right]$

Wasserstoffatom

Die Laguerre-Polynome haben eine Anwendung in der Quantenmechanik bei der Lösung der Schrödinger-Gleichung für das Wasserstoffatom bzw. im allgemeinen Fall für ein Coulomb-Potential. Mittels der zugeordneten Laguerre-Polynome lässt sich der Radialanteil der Wellenfunktion schreiben als

$R_{nl}(r) = D_{nl} \, \mathrm{e}^{-\kappa\,r} \, (2\,\kappa\,r)^l \, {\mathfrak L}_{n-l-1}^{2\,l+1}(2\,\kappa\,r)$

(Normierungskonstante D_nl, charakteristische Länge κ, Hauptquantenzahl n, Bahndrehimpulsquantenzahl l). Die zugeordneten Laguerre-Polynome haben hier also eine entscheidende Rolle. Die normierte Gesamtwellenfunktion ist durch

$\Psi_{n,l,m}(r, \vartheta, \varphi) = \sqrt{\frac{4\, (n-l-1)!}{(n+l)!\;n\,(n a_0/Z)^3}} \left[ \frac{2 r}{n a_0/Z} \right]^l \exp{\left\{ - \frac{r}{n a_0/Z} \right\}} \; {\mathfrak L}_{n-l-1}^{2l+1} \left( \frac{2r}{n a_0/Z} \right)\; Y_{l,m}(\vartheta, \varphi)$

gegeben, mit der Hauptquantenzahl n, Bahndrehimpulsquantenzahl l, magnetische Quantenzahl m, bohrschen Radius a₀ und Kernladungszahl Z. Die Funktion ${\mathfrak L}_n^l(r)$ sind die zugeordneten Laguerre-Polynome, und $Y_{l,m}(\vartheta, \varphi)$ sind die Kugelflächenfunktionen.

Weblinks

• http://mathworld.wolfram.com/LaguerrePolynomial.html
• http://www.ipf.uni-stuttgart.de/lehre/online-skript/mathe/p03.html
• Laguerresche Funktionen
• Radiale Wellenfunktionen, Laguerre-Polynome