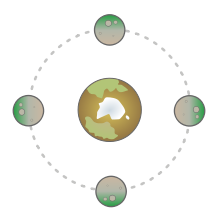
- Gebundene Rotation
-
Bei einer gebundenen Rotation ist vom Hauptkörper aus eine Seite des Satelliten ständig und die andere Seite – hier grün dargestellt – nie zu sehen.
Wegen der gebundenen Rotation sehen wir von der Erde aus nie diese Seite unseres Mondes.Die gebundene Rotation (Drehung) ist ein Begriff aus der Astronomie und beschreibt ein Phänomen zwischen zwei Himmelskörpern sehr unterschiedlicher Massen: Die Eigendrehung des massearmen Himmelskörpers ist hier nicht, wie üblich, unabhängig von der Umlaufperiode um den anderen, massereicheren Himmelskörper, sondern mit dieser Periode gekoppelt. Die gebundene Rotation tritt häufig bei Monden auf, die einen Planeten relativ nahe umkreisen, und hat beim Erdmond den zusätzlichen Effekt zufolge, dass wir von der Erde aus nie dessen Rückseite sehen können. Würde sich der Mond um sich selbst unabhängig von seiner Bewegung um die Erde herum drehen, sähen wir zwischendurch alle seine Seiten.
In den meisten Fällen von gebundener Rotation ist die Rotationsperiode des Himmelskörpers identisch zu seiner Umlaufzeit. Dadurch wendet der kleinere (rotationsgebundene) Himmelskörper dem massereicheren stets dieselbe Seite zu. Er dreht sich also während eines Umlaufs mit demselben Drehsinn auch genau einmal um seine Rotationsachse.
Das bekannteste Beispiel dafür ist das Erde-Mond-System: Der rotationsgebundene Erdmond wendet der Erde stets dieselbe Seite zu. Da die Mondbahn aber kein genauer Kreis ist, sind von der Mondrückseite im Laufe eines Monats schmale Randgebiete zu sehen (Libration).
Ein anderes Beispiel ist der Planet Merkur, der sich während seines 88-tägigen Umlaufs um die Sonne genau 1,5-mal dreht.
Von Korotation spricht man, wenn Umdrehung und Umlauf beider Himmelskörper jeweils aneinander angeglichen sind. Hierzu gehört das System Pluto-Charon, bei dem sich beide immer dieselbe Seite zuwenden.
Inhaltsverzeichnis
Ursache
Die Ursache gebundener Rotation ist die Bremsung der Rotation eines kleinen Himmelskörpers durch die Gezeitenreibung, die der von ihm umkreiste Zentralkörper bewirkt.
Durch die Gravitation des jeweils anderen Partners wird eine Gezeitenkraft ausgeübt, die den Himmelskörper zu einer länglichen Form in der Verbindungslinie der beiden Körper deformiert. Auf der dem anderen Himmelskörper zugewandten Seite entsteht ebenso ein Gezeitenberg wie auf der abgewandten Seite.
Solange der Himmelskörper noch nicht rotationsgebunden ist, wird der elongierte Körper aus der Verbindungslinie herausgedreht. Dadurch setzt ein Drehmoment an, das entgegengesetzt zur Drehrichtung und in Richtung der Verbindungslinie wirkt. Das Drehmoment erwirkt
- eine Verlangsamung der Rotation, sofern die Rotationsperiode kleiner als die Umlaufperiode ist, oder
- eine Beschleunigung der Rotation, sofern die Rotationsperiode größer als die Umlaufperiode ist.
Dieser Mechanismus wirkt bis zum Eintritt der gebundenen Rotation, die bei relativer Nähe nach einigen Jahrmillionen eintritt, bei entfernteren Himmelskörpern jedoch erst nach Jahrmilliarden oder nie.
Auswirkung auf die Bahn
Für das gesamte System gilt das Gesetz der Drehimpulserhaltung. Der Gesamtdrehimpuls setzt sich aus den Eigendrehimpulsen beider Körper (Rotation) und ihren Bahndrehimpulsen beim Umlauf um den gemeinsamen Schwerpunkt zusammen. Bei der Gezeitenreibung werden die Anteile der Rotation
- geringer, wenn die Rotationsperiode kleiner als die Umlaufperiode ist, was wegen der Erhaltung des Gesamtdrehimpulses ein Anwachsen des Bahnanteils und somit ein Anwachsen des Bahndurchmessers zur Folge hat, bzw.
- größer, wenn die Rotationsperiode größer als die Umlaufperiode ist, weshalb der Bahndurchmesser schrumpft.
Korotation
Grundsätzlich üben beide Partner ihre Gezeitenkraft aufeinander aus, sodass auch beide Himmelskörper rotationsgebunden sein können. Da jedoch häufig ein Partner eines Systems deutlich massereicher ist als der andere, ist die Gezeitenkraft ebenfalls ungleichmäßig verteilt, was zur Folge hat, dass die gebundene Rotation beim masseärmeren Partner zuerst eintritt.
Ist jedoch die Differenz beider Massen gering, so kann es zu einer beidseitigen Rotationsbindung kommen, der so genannten Korotation, bei der beide Partner dem jeweils anderen dieselbe Seite zeigen. Ein Beispiel hierfür ist das System Pluto-Charon.
Spin-Bahn-Resonanz
In einigen Fällen kann es zu einer Spin-Bahn-Resonanz kommen. Eine solche Resonanz liegt vor, wenn das Verhältnis der Umlaufperiode zur Bahnperiode durch zwei niedrige natürliche Zahlen ausgedrückt werden kann, z. B. 1:2 oder 3:2 und eine gravitative Bindung vorliegt.
Die Spin-Bahn-Resonanz tritt auf, wenn die Bahn vergleichsweise exzentrisch und die Gezeitenkraft relativ schwach ist. Durchläuft die Umlaufzeit des Begleiters während der Gezeitenbremsung den Bereich einer Resonanz zu seiner Bahnperiode, so kann die Rotationsperiode darin eingefangen werden, was dazu führt, dass eine weitere Abbremsung der Rotation unterbleibt.
Ein Beispiel hierfür ist der Merkur. Bei Merkur liegt eine 3:2-Resonanz vor, d. h. in der Zeit, in der Merkur dreimal rotiert, führt er zwei Sonnenumläufe aus.
Siehe auch
Literatur
- J. Audouze, Guy Israel: Cambridge Atlas of Astronomy. Cambridge University Press and Newnes Books, Cambridge 1985, ISBN 0-521-26369-7.
- C. D. Murray, S. F. Dermott: Solar System Dynamics. Cambridge University Press, Cambridge 2003, ISBN 0-521-57597-4.
Weblinks
Wikimedia Foundation.
