Gegenerde

Die Gegenerde (vom griechischen Antichthon, ὰντὶ=gegen und χθών=Erde) ist ein hypothetischer erdähnlicher Körper im kosmologischen Modell des antiken griechischen Philosophen Philolaos. Daneben gibt es auch die moderne Vorstellung, dass es einen unentdeckten Planeten geben könne, der dieselbe Umlaufbahn um die Sonne wie die Erde hat, sich jedoch auf der gegenüberliegenden Seite der Erde im Lagrange-Punkt L₃ hinter der Sonne befindet. Die Existenz eines solchen Planeten gilt heute als ausgeschlossen.

Das Konzept einer Gegenerde kommt auch in der modernen Science-Fiction-Literatur häufiger vor.

Die Gegenerde bei Philolaos

Skizze aus "Dante and the Early Astronomers" von M. A. Orr, 1913.

Der pythagoreische Philosoph Philolaos lehrte in der zweiten Hälfte des 5. Jahrhunderts vor Christus, dass es ein "Zentralfeuer" gebe, das den Mittelpunkt und Schwerpunkt des Universums bildet. Alle Dinge würden von diesem Mittelpunkt angezogen und alle Himmelskörper umkreisen ihn. Auf der innersten Bahn um das Zentralfeuer kreist die angenommene Gegenerde. Darauf folgen (von innen nach außen) Erde, Mond, Sonne, Merkur, Venus, Mars, Jupiter, Saturn und ganz außen die Fixsternsphäre. Bei ihrem Umlauf um das Zentralfeuer hat die (als flach gedachte) Erde eine gebundene Rotation, so dass sie dem Zentralfeuer immer die gleiche Seite zuwendet. Das Zentralfeuer ist für die Menschen damit immer "unten" und unsichtbar, da die bewohnte Seite der Erde dem Zentralfeuer stets abgewandt ist. Die Gegenerde wurde von Philolaos aus Balancegründen als Gegengewicht der Erde eingeführt. Dies hatte folgenden Hintergrund: die griechischen Philosophen stellten sich die Planeten als "leichte, ätherische" Objekte vor. Die Erde hingegen bestand aus Erde und Wasser und war damit zweifellos ein "schwerer" Körper. Wenn die Erde als einziger schwerer Himmelskörper das Zentralfeuer umkreist, wäre damit der Schwerpunkt des Universums nicht mehr im Mittelpunkt. Da dieser aber der Punkt ist, um den alles kreist, benötigte Philolaos' Modell einen zweiten Körper, der dieses durch die Erde verursachte Ungleichgewicht ausbalanciert: die Gegenerde.

Aristoteles kritisierte dieses System, da es nicht von den Erscheinungen, sondern von vorgefassten Ansichten ausgehe; die Gegenerde sei nur eingeführt worden, um die Zahl der bewegten Körper am Himmel auf zehn zu bringen, da diese Zahl als vollkommen galt. Aristoteles verwarf auch die These des "Zentralfeuers" und befürwortete statt dessen das geozentrische Weltbild, in dem die Erde im Mittelpunkt der Welt ruht und alle Himmelskörper sie umkreisen.

Adaption der These

Lagrange-Punkte

Im heliozentrischen Weltbild, dessen Wurzeln ebenfalls in der Antike liegen und das sich in Europa vor allem während der Renaissance allgemein durchsetzte, umkreisen alle Planeten, einschließlich der Erde, die Sonne. Eine hypothetische Gegenerde, die die Sonne auf derselben Bahn wie die Erde umkreist, jedoch der Erde entgegengesetzt, würde von der Erde aus gesehen immer "hinter der Sonne" stehen und wäre dadurch niemals sichtbar.

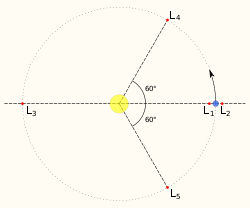
Joseph-Louis Lagrange berechnete, dass es im Dreikörperproblem fünf Punkte gibt, in denen ein Körper mit kleiner Masse kräftefrei ist. Einer von diesen fünf Punkten, L₃ genannt, befindet sich im System Sonne-Erde stets auf einer solchen Position und wäre damit ein physikalisch möglicher Aufenthaltsort für einen bisher unentdeckten Planeten.

Durch diese Überlegungen konnte sich die Annahme, dass eine solche Gegenerde existierte, zumindest als theoretisch denkbare Hypothese vereinzelt noch bis in die Neuzeit halten.

Probleme der These

Existierte ein solcher Planet tatsächlich, so wäre er stets hinter der Sonne verborgen. Er wäre jedoch trotzdem von der Erde aus auf Grund seines Gravitationseinflusses auf die anderen Planeten des Sonnensystems feststellbar. Es wurde kein solcher Einfluss festgestellt und Raumsonden zu den Planeten Venus, Mars und anderen Orten wären nicht an ihrem Ziel angekommen, wenn eine Gegenerde existierte, da ein solcher Einfluss nicht in die Berechnung der Flugbahn mit einbezogen wurde. Hinzu kommt, dass die Umlaufgeschwindigkeit der Erde aufgrund ihres elliptischen Orbits geringfügig variiert. Eine Gegenerde müsste sich also sehr präzise in einer bestimmten Umlaufbahn befinden, um ständig hinter der Sonne zu bleiben.

Die Umlaufbahn einer Gegenerde wäre zudem in einer geologisch relativ kurzen Zeitspanne instabil und würde aus der exakten Gegenposition zur Erde wegwandern. Dies würde dazu führen, dass die beiden Planeten entweder zusammenstießen oder sehr nahe aneinander vorbeiflögen, was dazu führen würde, dass beide Planeten aus ihrem bisherigen Orbit geworfen würden. Eine Gegenerde kann sich auch nicht in den stabilen Lagrange-Punkten L₄ beziehungsweise L₅ befinden (wie der hypothetische Planet Theia), welche in der Bahn der Erde 60° vor beziehungsweise 60° hinter der Erde liegen, da in diesen Lagrange-Punkten nur Körper mit im Verhältnis zu den anderen beiden großen Körpern verschwindend kleiner Masse positioniert werden können (Trojaner).

Das Dreikörperproblem erlaubt prinzipiell keine über lange Zeiträume stabile Bewegung zweier Planeten in derselben Entfernung vom Zentralgestirn. Lediglich leichte Objekte wie Asteroiden können sich längerfristig in den Lagrange-Punkten L₄ und L₅ eines Planeten aufhalten.

Die Gegenerde in der Science Fiction

In der Science-Fiction-Literatur wird das Konzept der Gegenerde gelegentlich aufgegriffen, zum Beispiel im Gor-Zyklus von John Norman und in der Serie Weltraumpartisanen von Nikolai von Michalewsky.

Die zweite Erde

Von der Gegenerde zu unterscheiden ist eine mögliche zweite Erde, d. h. ein erdähnlicher Planet unter den bisher rund 450^[1] entdeckten und weiteren vermuteten Exoplaneten jenseits des Sonnensystems.

Weblinks

• http://www.drury.edu/ess/History/Ancient/pythagoreans1.html (Englisch)

Einzelnachweise

1. ↑ GEO. 06/2010, S. 90.

Literatur

• Petra Hartmann: Der Traum vom zehnten Planeten. Eine kurze Geschichte der Gegenerde in Philosophie, Film und Phantastik. Nachwort zu: Mark Brandis: Der Spiegelplanet. Nittendorf, Wurdack, 2010. S. 163–190.